4 La théorie
L’analyse des durées peut être vue comme l’étude d’une variable aléatoire \(T\) qui décrit la durée d’attente jusqu’à l’occurence d’un évènement.
- La durée \(T=0\) est le début de l’exposition au risque (entrée dans le Risk set).
- \(T\) est une mesure non négative de la durée.
La principale caractéristique de l’analyse des durées est le traitement des informations dites censurées, lorsque la durée d’observation est plus courte que la durée d’exposition au risque.
4.1 Temps et durée
Le temps est une dimension (la quatrième), la durée est sa mesure. La durée est tout simplement calculée par la différence, pour une échelle temporelle donnée, entre la fin et le début d’une période d’exposition ou d’observation.
On distingue généralement deux types de mesure de la durée : continue et discrète/groupée. Ces deux notions ne possèdent pas réellement de définition, la différence s’explique plutôt par la présence ou non de simultanéité dans l’occurrence des évènements. Le temps est intrasèquement continu car deux évènements ne peuvent pas avoir lieu en « même temps ». C’est donc l’échelle temporelle choisie ou imposée par l’analyse et les données qui pourra rendre cette mesure continue ou discrète/groupée. Pour un physicien travaillant sur la théorie de la relativité avec des horloges atomiques, une minute (voire une seconde) est une mesure très groupée pour ne pas dire grossière du temps, alors que pour un géologue c’est une mesure continue. Pour ces deux disciplines, cette échelle de mesure n’est pas adaptée à leur domaine. Le choix de l’échelle temporelle doit être pertinent par rapport aux objectifs de l’analyse même si on dispose des informations très fines (dates de naissance exactes). Etudier la fécondité avec une métrique journalière qui n’aurait pas de sens.
Il existe des situations où les durées sont par nature discrète, lorsqu’un évènement ne peut avoir lieu qu’à un moment précis (date d’anniversaire des contrats pour l’analyse des résiliations). Généralement dans les sciences sociales avec un recueil de données de type rétrospectif, les mesures dites discrètes sont plutôt de nature groupées. Pour une même année, on considèrera indifféremment des évènements qui se produiront un premier janvier ou un 31 décembre d’une même année.
- Durée continue : absence (ou très peu) d’évènements mesurés simultanément
- Durée discrète/groupée : présence constante et/ou en grand nombre d’évènements simultanés
4.2 Le Risk Set
- Il s’agit de la population soumise ou exposée au risque lorsque \(T=t_i\).
- Cette population varie dans le temps car:
- Certaines personnes ont connu l’évènement, donc ne peuvent plus être soumises au risque (ex: décès si on analyse la mortalité).
- Certaines personnes sortent de l’observation sans avoir (encore) observé l’évènement: décès si on analyse un autre type d’évènement, perdu.e.s de vue, fin de l’observation dans un recueil rétrospectif.
4.3 La Censure
Une observation est dite censurée lorsque la durée d’observation est inférieure à la durée d’exposition au risque
4.3.1 Censure à droite
Définition
Certains individus n’auront pas (encore) connu l’évènement à la date de l’enquête après une certaine durée d’exposition. On a donc besoin d’un marqueur permettant de déterminer si les individus n’ont pas observé l’évènement sur la période d’étude.
Pourquoi une information est-elle censurée (à droite)?
- Fin de l’étude, date de l’enquête.
- Perdu de vue, décès si autre évènement étudié.
En pratique (important)
- Ne pas exclure ces observations, sinon on surestime la survenue de l’évènement.
- Ne pas les considérer a-priori comme sorties de l’exposition sans avoir connu l’évènement. Elles peuvent connaître l’évènement après la date de l’enquête ou en étant perdues de vue. Sinon on sous-estime la durée moyenne de survenue de l’évènement.
Exemple
On effectue une enquête auprès de femmes : On souhaite mesurer l’âge à la naissance de leur premièr enfant. Au moment de l’enquête, une femme est âgée de 29 ans n’a pas d’enfant.
Cette information sera dite «censurée».
Elle est clairement encore soumise au risque après la date de l’enquête. Au niveau de l’analyse, elle sera soumise au risque à partir de ses premières règles jusqu’au moment de l’enquête.
La question se posera différemment si la personne à 75 ans et n’a pas d’enfant, car elle sera sortie de l’exposition au risque.
Hypothèse fondamentale
Les observations censurées ont vis à vis du phénomène observé le même comportement que les observations non censurées. On dit que la censure est non informative. Elle ne dépend pas de l’évènement analysé. Normalement le problème ne se pose pas dans les recueil retrospectif.
Problème posé par la censure informative
Par exemple en analysant des décès avec un recueil prospectif, si un individu est perdu de vue en raison d’une dégradation de son état de santé, l’indépendance entre la cause de la censure et le décès ne peut plus être assurée.
- A l’Ined l’exploitation du registre des personnes atteintes de mucoviscidose (G.Belis) donne une autre illustration de ce phénomène. Chaque année un nombre significatif de personnes sortent du registre. On pas les résultats des examens annuels qu’ils doivent subir. Si certain.e.s perdu.e.s de vue s’expliquent par des déménagements, émigration ou par un simple problème d’enregistrement des informations (le médecin a oublié), on note qu’ils/elles sont nombreu.se.s à présenter une forme « légère » de la maladie. Cette information étant être donnée ici par la mutation du gène. Comme il n’est pas recommandé de supprimer ou de traiter ces observations comme des censures à droite non informatives, on peut les appréhender comme un risque concurrent au décès ou à tout autre évènement analysé à partir de ce registre (voir section dédiée).
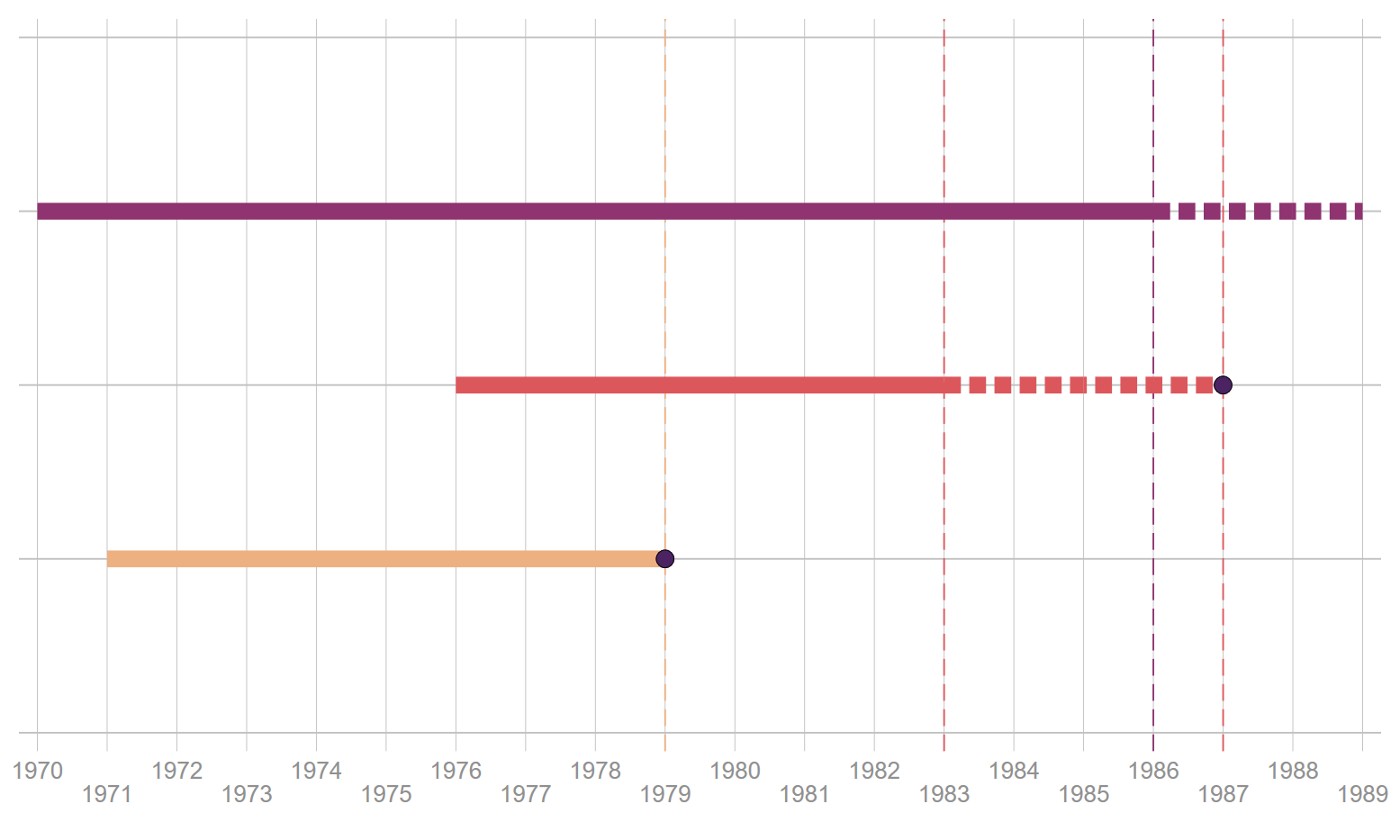
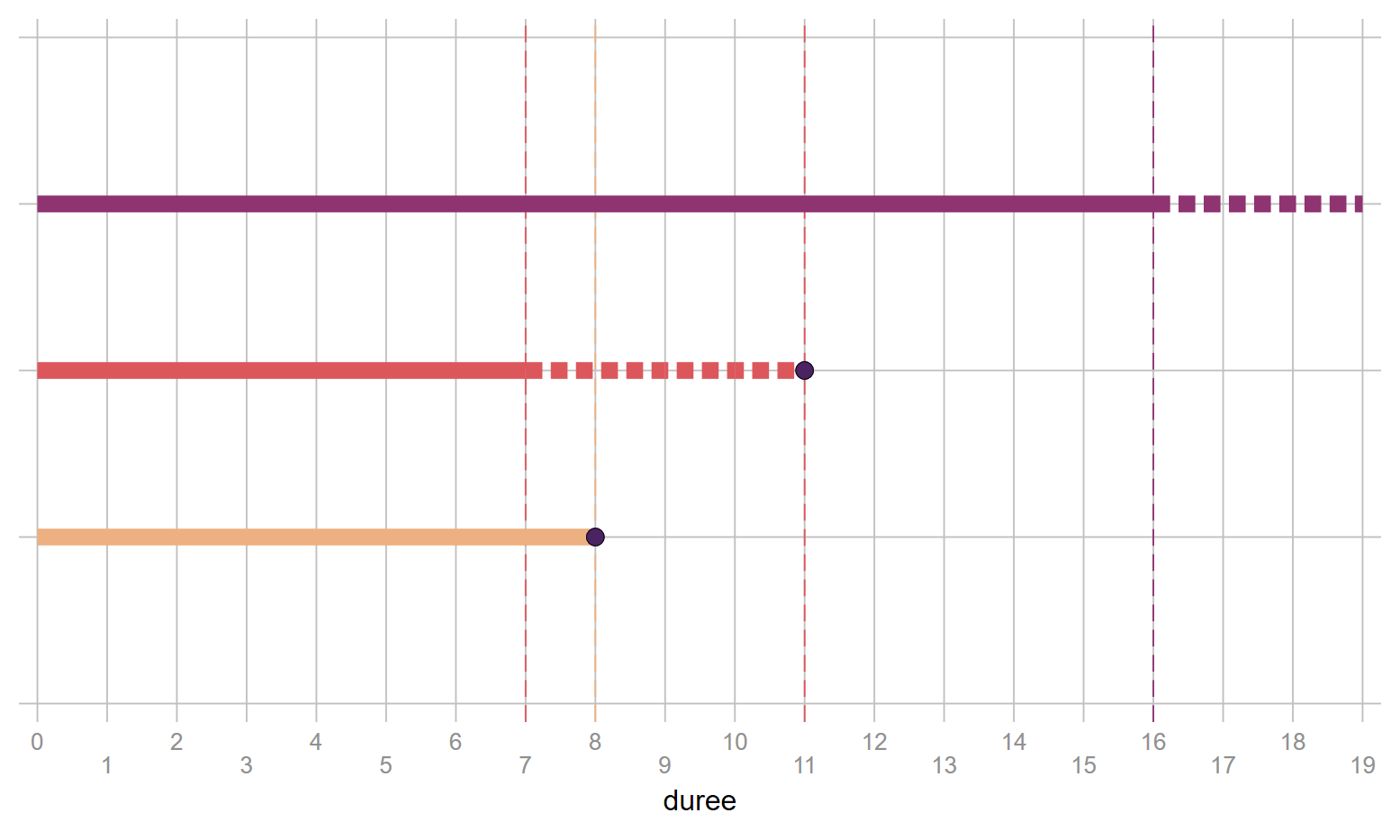
Les graphiques suivant représentent, en temps calendaire et après sa transformation en durée, la logique des censures à droite. Le recueil des informations est ici de nature prospectives, et bien évidemment on suppose que le début de l’observation correspond à un début d’exposition cohérent avec l’analyse réalisée (année de diagnostic d’une maladie, début d’une séquence d’emploi, de lieu de résidence, de couple ou de célibat strict etc….).
- Trait plein : Durée observée
- Pointillés : Durée censurée
- Bulle : moment de l’évènement
4.3.2 Censure à gauche, troncature et censure par intervalle
Censure à gauche
L’évènement a pu se produire avant le début période d’observation, mais on est pas en mesure de savoir s’il s’est produit, et si on sait qu’il s’est produit on est pas en mesure de savoir quand. Typique des données prospectives, de type registre, avec par exemple des âges à l’inclusion différenciés. La présence de ce type de censure ne permet de définir lors de la création de l’échantillon d’analyse des durées d’exposition cohérente pour l’ensemble de observations de départ. Même si elle ne sont pas traitée dans ce support, il existe quelques méthodes, en durée continue seulement, pour obtenir des résultats en présence de ce type de censure, mais à la condition qu’elle ne soit pas trop nombreuses. On peut également filtrer l’échantillon en amont en conservant seulement celles dont le début d’exposition est clairement défini1.
Censure par intervalle
Traditionnellement la censure par intervalle est définie par l’impossibilité de dater exactement la survenue d’un évènement dans un intervalle de temps2. Dans ce sens, on pourrait donc affirmer qu’elle est une caractéristique propre aux temporalité groupées dites à durée discrète3. On peut sans problème généraliser ce phénomène de censure à l’occurence: un évènement peut se produire entre 2 temps d’observations sans qu’on puisse l’observer. Un exemple classique en criminologie est celle de la récidive d’un délit entre deux arrestations ou deux condamnation: on sait qu’une personne a récidivé en raison de son arrestation, mais on est pas en mesure de savoir s’elle a récidivé plus tôt….car pas vu pas pris. A noter également, toujours dans un recueil prospectif, qu’un phénomène de censure à droite lié aux perdu.e de vue peut se transformer en censure par intervalle lorsque la personne “réapparait” et est de nouveau incluse à l’échantillon4.
Troncature
Par l’exemple, on analyse la survie d’une population. Seule la survie des individus vivants à l’inclusion peut être analysée (troncature à gauche). On peut donc rencontrer un phénomène de sélection difficilement contrôlable.
Un exemple: dans l’enquête Virage, on a des informations sur les tentatives de suicide. Seule l’analyse des tentatives de suicide n’ayant pas entrainé le décès peuvent être analysé.
Durée d’observation supérieure à la durée d’exposition
A l’inverse de la censure, des individus peuvent sortir de l’exposition avant la fin de la période d’observation, et il convient donc de corriger la durée de cette sortie.
- Si au moment de l’enquête une femme sans enfant a 70 ans, cela n’a pas de sens de continuer de l’exposer au risque au-delà d’un certain âge. Si on ne dispose pas d’information sur l’âge à la ménopause on peut tronquer la durée un peu au-delà de l’âge le plus élevé à la première naissance observée dans les données.
- Situation traitée dans le TP de la formation: on analyse la durée de la première séquence d’emploi ou d’une suite de séquence d’emploi sans rupture (chômage, maladie, sortie du marché du travail etc…). Il conviendra pour les personnes qui n’on pas connu de rupture (d’au moins un an par exemple) de faire sortir certaines personnes au moment de la retraite et non au moment de l’enquête, si elle sont déjà retraitées lors du recueil. Compte tenu des générations enquêtées, plutôt anciennes, on pourra considérer ces âges à la retraite comme des âges à censures à droites non informatives.
4.4 Les grandeurs
4.4.1 Les grandeurs utilisées
La fonction de survie: \(S(t)\)
La fonction de répartition: \(F(t)\)
La fonction de densité: \(f(t)\)
Le risque instantané: \(h(t)\)
Le risque instantané cumulé: \(H(t)\)
Remarques:
- Toutes ces grandeurs sont mathématiquement liées les unes par rapport aux autres. En connaître une permet d’obtenir les autres.
- Au niveau formel on se placera ici du point de vue où la durée mesurée est strictement continue. Cela se traduit, entre autre, par l’absence d’évènements dits “simultanés”. En présence de durée discrète/groupé, il est a noté que les expressions se simplifie, en particulier pour la densite ou le risque dit instantané.
- Les expressions qui vont suivre ne sont pas des estimateurs, mais des grandeurs dont on précisera seulement les propriétés. Ce sont les techniques d’estimations, et la cohérence des données avec la théorie, qui devront respecter ces propriétés .
4.4.2 La fonction de Survie \(S(t)\)
Dans ce type d’analyse, il est courant d’analyser la courbe dite de survie. Hors contexte de mortalité on peut lui préférer la notion de courbe de séjour (Courgeau, Lelièvre).
La fonction de survie donne la proportion de la population qui n’a pas encore connue l’évènement après une certaine durée \(t\). Elle y a donc “survécu”.
Formellement, la fonction de survie est la probabilité de survivre au-delà de \(t\), soit:
\[S(t) = P(T>t)\]
Propriétés:
- \(S(0)=1\)
- \(\lim\limits_{t\to{\propto}}S(t)=0\)
La fonction de survie est donc strictement non croissante.
4.4.3 La fonction de répartition \(F(t)\)
C’est la probabilité de connaitre l’évènement jusqu’en \(t\), soit:
\[F(t)=P(T\leq{t})\]
Soit: \(F(t) = 1 - S(t)\)
La fonction de survie et la fonction de répartition sont donc deux grandeurs strictement complémentaires, pour ne pas dire identique, et décrivent la même information.
Propriétés:
- \(F(0)=0\)
- \(\lim\limits_{t\to{\propto}}F(t)=1\)
4.4.4 La fonction de densité \(f(t)\)
- Pour une valeur de \(t\) donnée, la fonction de densité de l’évènement donne la distribution des moments où les évènement ont eu lieu. Le numérateur donne classique, densité oblige, la probabilité de connaitre l’évènement dans un petit intervalle de temps \(dt\). Si \(dt\) est proche de 0 (temps continu) alors cette probabilité tend également vers 0. On norme donc cette probabilité par \(dt\). Rappel: on est toujours ici dans la théorie.
- En temps continu, la fonction de densité est donnée par la dérivée de la fonction de répartition: \(f(t)=F'(t)=-S'(t)\). On reste dans des relations statisques élémentaires… mais cette densité n’est pas formellement une probabilité. Il s’agit plutôt d’un taux.
Formellement la fonction de densité \(f(t)\) s’écrit:
\[f(t)=\lim\limits_{dt\to{0}} \frac{P(t\leq{T}< t + dt)}{dt}\]
4.5 Le risque instantané \(h(t)\)
Concept fondamental de l’analyse des durées:
\[h(t)=\lim\limits_{dt\to{0}} \frac{P(t\leq{T}< t + dt | T\geq{t})}{dt}\]
- \(P(t\leq{T}< t + dt | T\geq{t})\) donne la probabilité de survenue de l’évènement sur l’intervalle \([t,t+dt[\) conditionnellement à la survie au temps \(t\).
- En divisant par \(dt\), La quantité obtenue donne alors un nombre moyen d’évènements que connaîtrait un individu durant un très court intervalle de temps.
- A priori cette quantité n’est pas une probabilité. C’est la nature de l’évènement, en particulier sa non récurrence, et la métrique temporelle choisie ou disponible qui peut la rendre assimilable à une probabilité. Tout comme la densité, on est plutôt dans la définition d’un taux (d’où l’expression hazard rate en anglais… traduction ???? taux de risque ????).
On peut également écrire:
\(h(t)=\frac{f(t)}{S(t)}=\frac{F'(t)}{S(t)}=-\frac{S'(t)}{S(t)}\) 5
On remarque que cette fonction de risque (ou hazard rate) n’est pas une probabilité car \(\frac{f(t)}{S(t)}\) ne peut pas contraindre ici la valeur obtenue à ne pas être supérieure à 1.
Les expressions de la densité et du risque dit instantané se simplifient: \(f(t)=P(t\leq{T}< t + dt)\) et \(h(t)=P(t\leq{T}< t + dt | T\geq{t})\). Ces deux grandeurs ne sont plus des taux tel qu’ils ont été définit précedemment, mais des probabilités. En durée discrète, on aurait donc \(dt=1\)
Néanmoins les relations entre les grandeurs, en particulier celle qui lie risque, densité et survie reste toujours valable. Ceci est fondamental, car elle permet de définir la fonction de vraisemblance sur laquelle repose le calcul de tous les estimateurs.
Illustration du concept
Cette notion de taux de risque ou hazard rate non réductible à un probabilité, est à mon sens très bien illustré par G.Colletaz dans ces notes de cours (pages 11-12). Dans ce qui suit, j’en fais un quasi copier-coller. En se positionnant sur des échelles temporelles plus facilement saisissables pour la description de phénomènes socio-démographiques (on supprime la limite des expressions données pour \(f(t)\) et \(h(t)\).
On s’intéresse au risque d’attraper un rhume durant les mois d’hiver, disons entre le 1er janvier et le 1er avril [3 mois]. La probabilité, que l’on considèrera constante, d’attraper un rhume chaque mois est de 48% (il s’agit bien évidemment d’un risque). Quel est le risque d’attraper un rhume durant l’unité de temps qu’est cette saison froide de 3 mois?
\(\frac{0.48}{1/3}=1.44\). On peut donc s’attendre a attraper 1.44 rhume durant la période d’hiver. Il s’agit bien là d’un risque.On passe une année en vacances dans une région, franchement pas très accueillante, où la probabilité de décéder chaque mois est évaluée à 33%. Quel est le risque de décéder pendant cette année? \(\frac{0.33}{1/12}=3.96\)
On le voit, cette mesure du risque peut donc être supérieure à 1. En soit cela ne pose pas de problème comme il s’agit d’un nombre moyen d’évènements espérés, mais pour des évènements qui ne peuvent pas se répéter, évènements dits absorbants (par définition la mortalité), l’interprétation n’est pas très intuitive.
Le risque étant constant dans chaque intervalle (mois), on peut prendre son inverse qui va mesurer la durée moyenne (espérée) jusqu’à l’occurence de l’évènement.
Par analogie seulement, on retrouve ici un concept classique en analyse démographique comme l’espérance de vie (survie): la question n’est pas de savoir si on va mourir ou non, ce risque inconditionnellement à la durée étant par définition égal à 1, mais jusqu’à quand on peut espérer (sur)vivre.
- Pour le rhume, la durée moyenne est de \(1.44^{-1}=0.69\) du trimestre hivernal. On peut donc s’attendre, en moyenne, à attraper un rhume approximativement au début du mois de mars. Bien évidemment, certain.e.s attraperons un rhume avant, certaine.s après, certain.e.s aucun6.
- Pour l’année sabbatique, la durée moyenne de survie est de \(3.96^{-1}=0.25\) d’une année soit 3 mois après l’arrivée dans la région.
4.5.1 Le risque cumulé \(H(t)\)
Le risque cumulé est égal à :
\[H(t)=\int_{0}^{t} h(u)du = -log(S(t))\]
On peut alors réécrire toutes les autres quantités à partir de celle-ci:
- \(S(t)=e^{-H(t)}\)
- \(F(t)=1-e^{-H(t)}\)
- \(f(t)=h(t)\times{e^{-H(t)}}\)
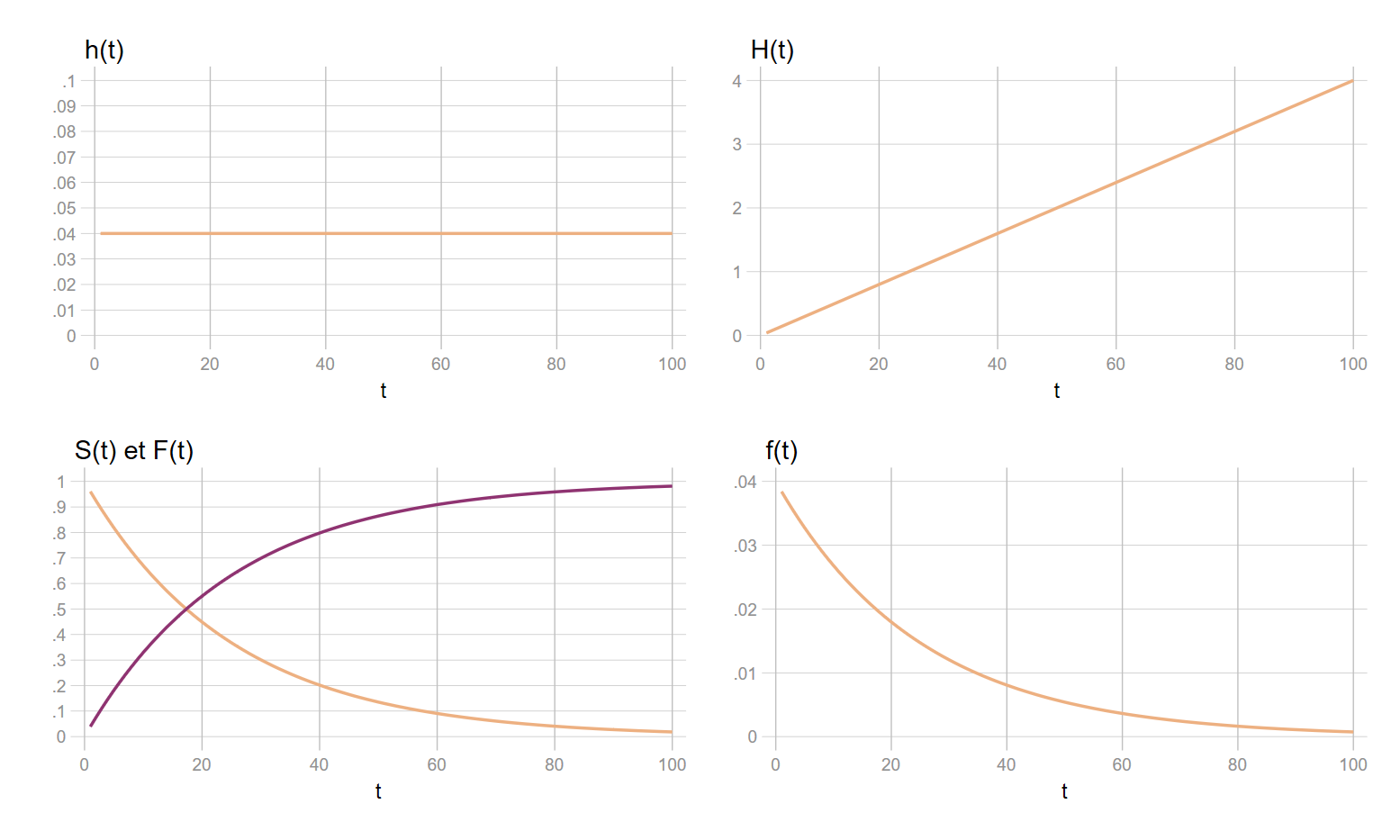
Exemple avec la loi exponentielle (risque constant)
Si on pose que le risque (ou taux de risque) est strictement constant au cours du temps: \(h(t)=a\), on dira qu’il suit une loi exponentielle. Cette situation est, par exemple, typique des processus dits sans mémoire comme la durée de vie des ampoules. Sans trop de difficulté, toutes les expressions peuvent être formellement définies:
- \(h(t)=a\)
- \(H(t)=a\times{t}\)
- \(S(t)=e^{-a\times{t}}\)
- \(F(t)=1-e^{-a\times{t}}\)
- \(f(t)=a\times{e^{-a\times{t}}}\)
Exercice
- On a une population de 100 cochons d’Inde.
- On analyse leur mortalité (naturelle).
- Ici l’analyse est en temps discret.
- La durée représente le nombre d’année de vie.
- Il n’y a pas de censure ou troncature à droite.
| Durée | Nombre de décès |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 3 |
| 4 | 9 |
| 5 | 30 |
| 6 | 40 |
| 7 | 10 |
| 8 | 3 |
| 9 | 2 |
| 10 | 1 |
N=100
A quel âge le risque de mourir des cochons d’Inde est-il le plus élevé? Et quelle est sa valeur?
4.6 Remarques complémentaires
4.6.1 Formes typiques de la fonction de survie
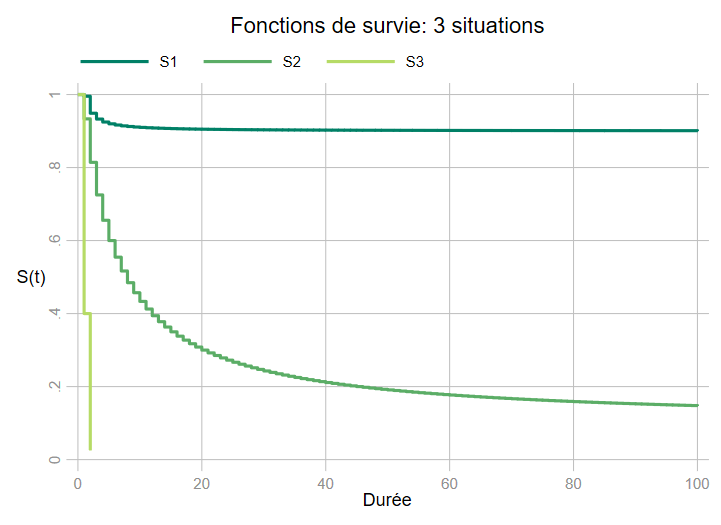
Une des propriétés de la fonction de survie ou de séjour est qu’elles tendent vers 0. A la lecture du graphique suivant, cela peut correspondre à la forme de la courbe S2, bien que le % de survivant tend à baisser de moins en moins à mesure que la durée augmente. Deux cas limites doivent être considéré.
Par anticipation, on peut déjà signalée que les fonctions de séjours qui sont représentées ci-dessous, font l’objet d’une estimation de type Kaplan-Meier.
S1: très peu d’évènements et la fonction de séjour suit une asymptote nettement supérieur à 0 ( \(\lim\limits_{t\to{\propto}}S(t)=a\) avec \(a>0\)). La question est plus délicate car on interroge l’exposition au risque d’une partie de l’échantillon ou, dit autrement on peut penser qu’une fraction est immunisé au risque. Cette problématique est rapidement posée en fin de formation.
S2: la situation attendue
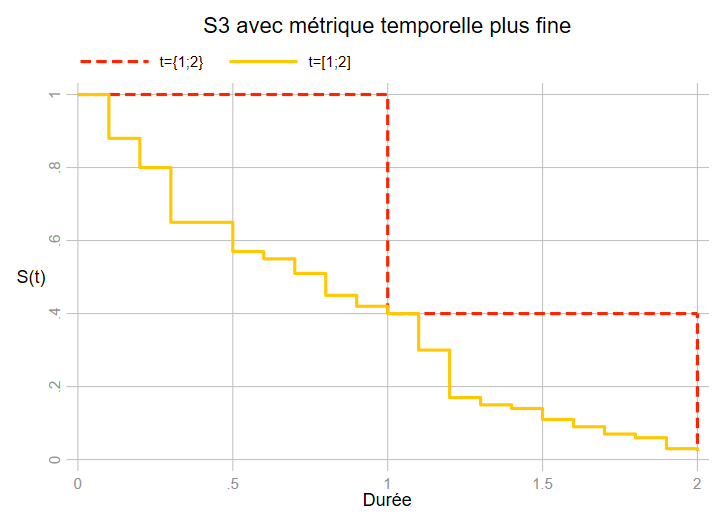
S3: La survie tombe à 0 très/trop rapidement: il n’y a donc pas ou presque pas de durée (par exemple presque tout l’échantillon observe l’évènement la première année de l’exposition). Si on dispose d’une information plus fine pour dater les évènements, la fonction de séjour pourra reprendre une forme plus “standard”. Dans le graphique précédent \(S(t=1)=0.4\) , \(S(t=2)=0.025\), mais si on dispose par exemple de 10 points d’observations supplémentaires dans chaque intérevalle groupé:
4.6.2 Absence de censures à droites
Les méthodes qui vont être présentées plus tard gèrent la présence de censures à droite. En leur absence, elles restent néanmoins parfaitement valables. L’absence de censure facilite certaines analyses, par exemple celles des fonctions de séjour où le calcul direct des durées moyennes est rendu possible. On peut alors utiliser d’autres méthodes plus, en première intentions plus simples, en analysant directement la distribution des évènement dans le temps. La durée ou une fonction de celle-ci pouvant être directement passées comme variable dépendante.
4.6.3 Utilisation des pondérations dans un schema retrospectif avec des biographies longues
Cette problématique mériterait au moins une section propre. Mais le sujet est compliqué et sensible. En attendant mieux, je rajoute quelques éléments.
L’argumentaire écrit à la suite cet encadré est antérieur à septembre 2024. depuis des questionnements m’ont été adressés par l’équipe de groupe d’exploitation de l’enquête Envie… et il peuvent remettre un peu en cause cet argumentaire, la plage d’âges de l’enquête étant assez réduite (de 18 à 29 ans). Plus précisément, la question portait sur l’utilisation des pondérations dans l’estimation non paramétrique des courbes de survies.
Pour ce qui est des modèles, en sciences sociales les variables entrant dans le calcul des pondérations sont généralement introduites dans les modèles, et à moins de renvendiquer une analyse de type Population average, l’ajout des pondérations ne s’impose pas. Quel est le sens d’un Population average en analyse des durées lorsqu’on s’éloigne d’une plage d’observation très courte, comme un suivi sur 12 mois de reprises d’emploi de personnes au chômage ????
Dans les domaines où s’appliquent régulièrement l’analyse des durées, à savoir la médecine et l’épidémiologie, la question des pondérations se pose lors d’études rétrospectives avec de fort soupçons d’effet de sélection (unbalanced data). En médecine on procède généralement à un recueil permettant d’appliquer directement des méthodes case-control, qui permet justement de contourner le problème. La problématique de la pondération ne se pose donc pas pas en terme de représentativité dans une population générale, mais en terme d’effet confondant, soit l’absence ou la mauvaise mesure hors redressement par la pondération d’une caractéristique corrélée à une covariable mais également à l’évènement qu’on analyse.
Caractéristique de l’analyse des durées: la taille de l’échantillon se réduit au cours du temps par le jeu des censures et des évènements. Question: de quoi elles sont représentatives tout du long de la plage d’observation, alors quelles ont été calculées au moment de l’enquête, schema classique pour les enquêtes en population générale.
Dans la courte bibliographie accessible que j’ai donné en début de support, la question n’est pas traitée ni par G.Colletaz ni par S.Quantin (pourtant Insee)… Je marche seul!!!!
Note bien compliquée comme il le faut de T.Therneau et al… champ médecine]
- Les informations permettant de calculer la pondération sont issus du recensement américain de 2000…le début du suivi commence au milieu des années 90. Mais l’analyse y est rétrospective. Les différentes techniques de pondération qui sont discutées cherchent à recalibrer l’échantillon pour contrôler le plus correctement possible la présence d’un effet de confusion avec l’âge. Il ne s’agit pas d’une analyse en population générale, ce qui n’aurait pas de sens vu qu’on analyse la survie à une maladie du sang.
[Eléments rédigés avant septembre 2024]
Une question assez récurrente concerne l’utilisation des poids de sondage dans les analyses de durées avec longueurs biographiques souvent assez longues. Leur utilisation ne me semble pas recommandée voire à exclure sauf exceptions. En effet les pondérations sont générées au moment de l’enquête, alors que les évènements étudiés peuvent remonter dans un passé plus ou moins lointain pour une partie de la population analysée. Si on regarde de plus près, la création de poids longitudinaux ne résoudrait pas grand chose, les pondérations devant être recalculées à chaque moment d’observation ou à chaque moment où des évènements se produisent. Par ailleurs on mélangerait régulièrement à un instant donné des personnes issues de générations tellement éloignées que cela rend impossible tout calage sur des caractéristiques d’une population à un instant t. Supposons une personne âgée de 25 ans et un personne âgée de 70 ans au moment de l’enquête en 2022, avec un début d’observation à l’âge de 18 ans . A 20 ans (\(t=2\)), pour la première personne les caractéristiques de la population sont celles de 2017, pour celle de 70 ans celles de 1972. On fait comment??????
Ce qui a été fait dans le projet worklife pour Air France↩︎
Garder en mémoire que l’analyse des durées ou de survie a été très largement développé dans un carde à durée continue↩︎
Si on utilisee une mesure de la durée sur l’âge, on ne sait pas si l’évènement à eu lieu le lendemain de l’anniversaire ou la veille de l’anniversaire suivant↩︎
Voir exemple plus haut sur le registre de la mucoviscidose↩︎
La relation \(h(t)=\frac{f(t)}{S(t)}\) et donc \(f(t)= h(t) \times S(t)\) est intéressante et importante car elle permet d’écrire la vraisemblance du processus probabiliste permettant d’estimer les paramètres des différentes analyses. On voit déjà sa proximité avec la fonction de masse de Bernouilli: \(f(y_i) = p^{y_i} \times (1-p)^{1-y_i}\). Se reporter à la section qui décrit qui la vraisemblance partielle de Cox pour s’en faire une idée plus précise.↩︎
et une analyse plus fine pourrait s’intéresser sur l’effet du port du masque sur ce risque d’attraper le rhume↩︎