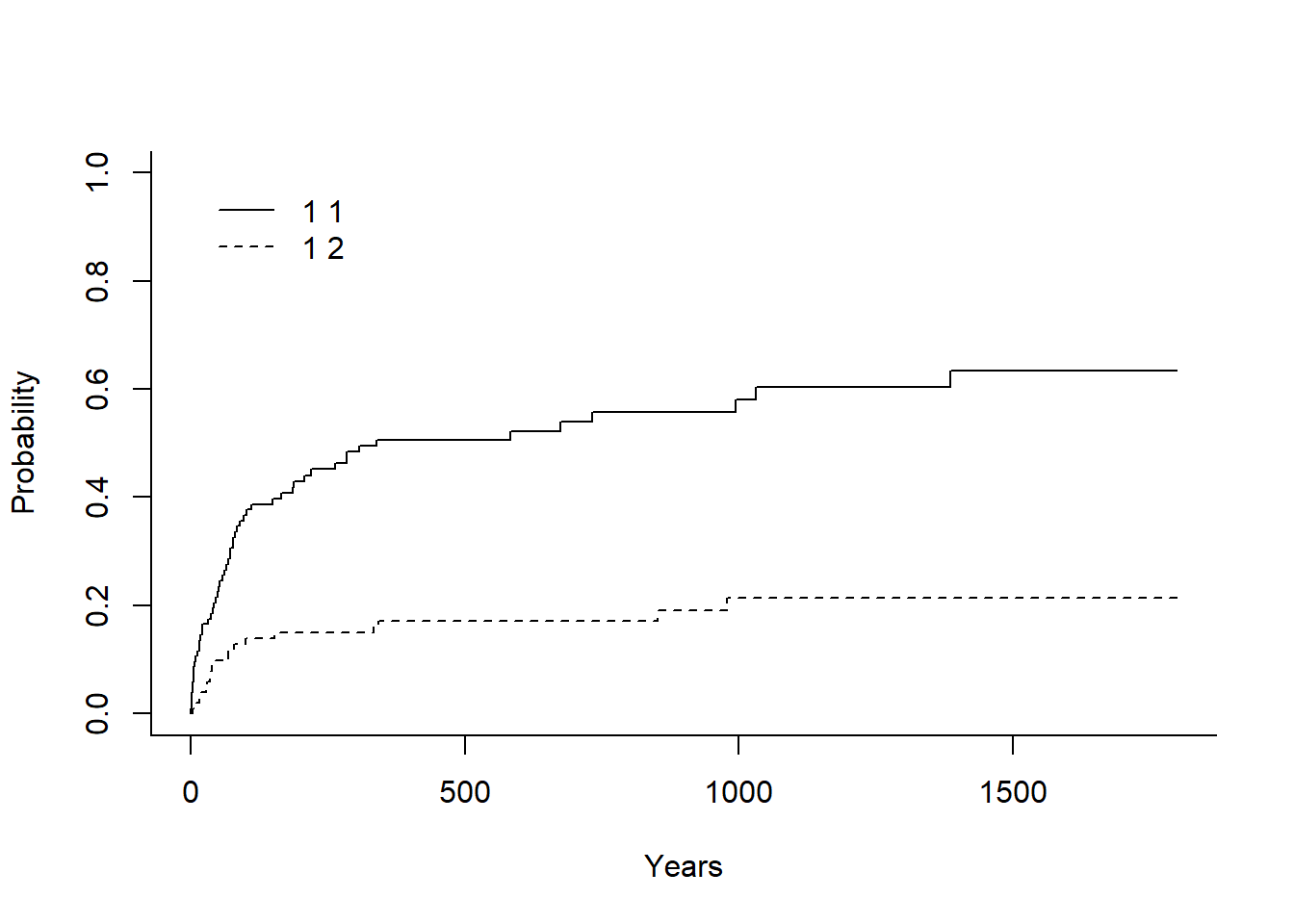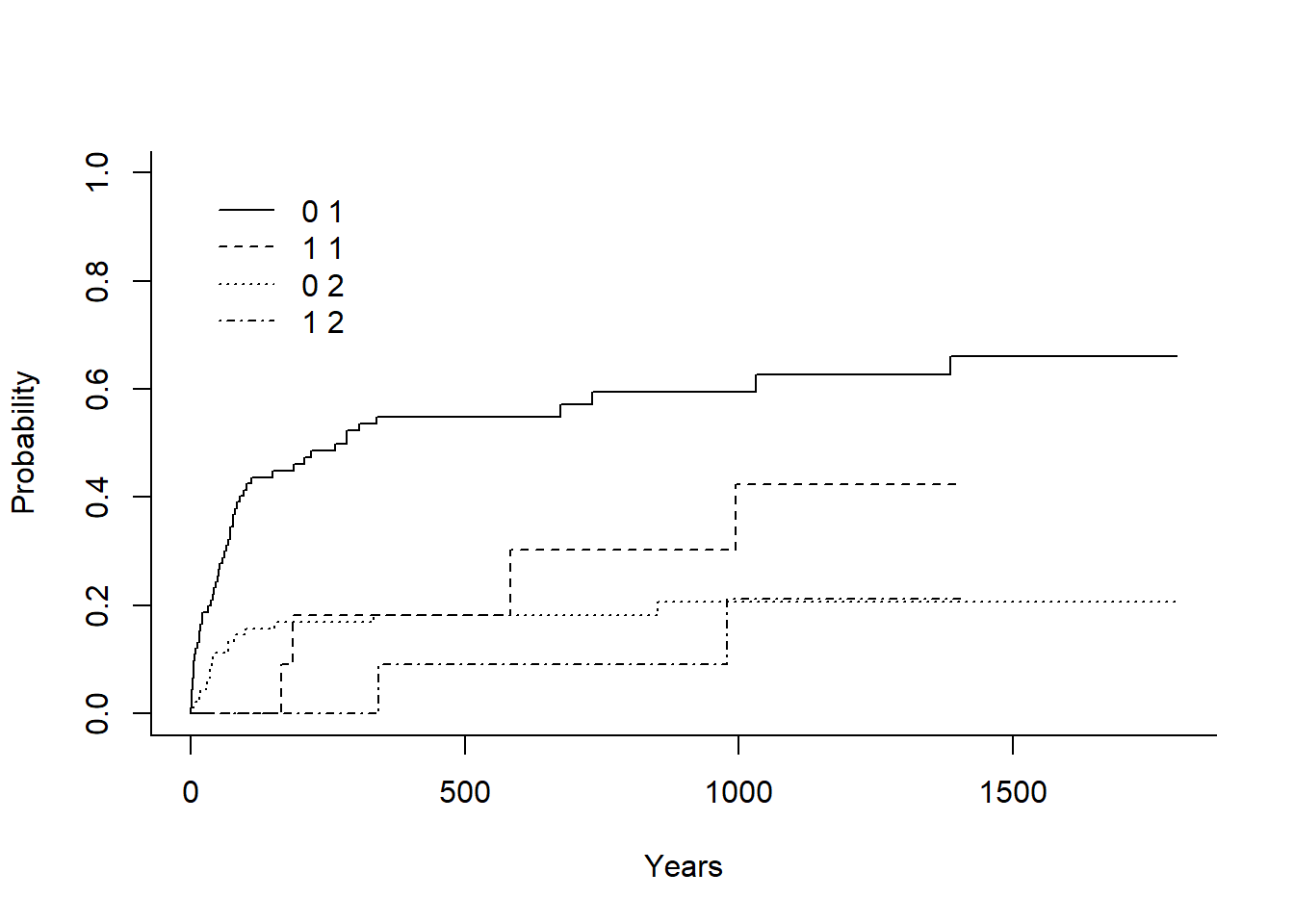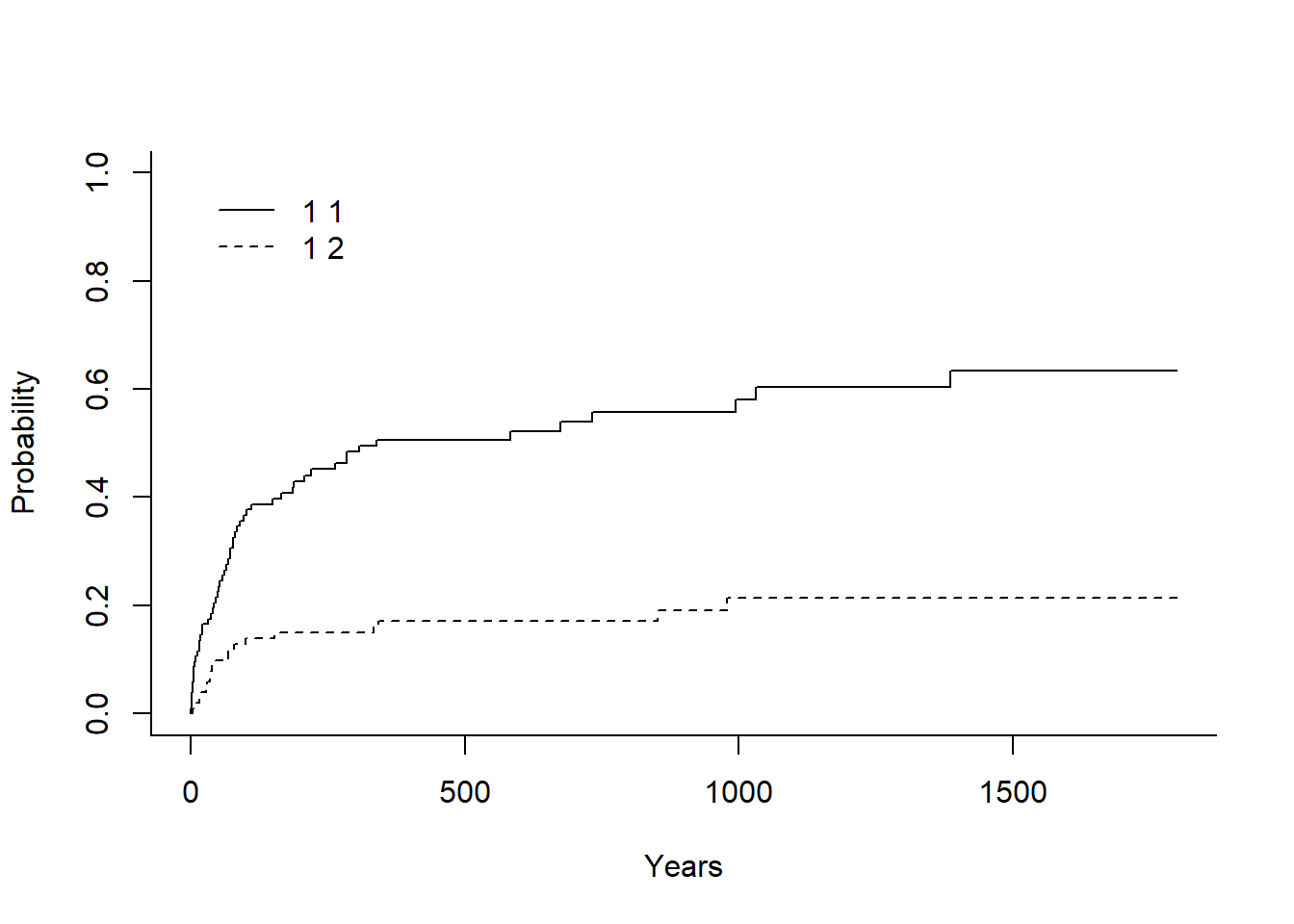#install.packages("survival")
#install.packages("survminer")
#install.packages("flexsurv")
#install.packages("survRM2")
#install.packages("tidyr")
#install.packages("dplyr")
#install.packages("jtools")
#install.packages("gtools")
#install.packages("cmprsk")
#install.package("gtsummary")
#install.packages("muhaz")
#install.packages("nnet")
library(survival)
library(survminer)
library(ggsurvfit)
library(flexsurv)
library(survRM2)
library(tidyr)
library(dplyr)
library(jtools)
library(gtools)
library(cmprsk)
library(discSurv)
library(gtsummary)
library(muhaz)
library(nnet)15 R
Programme de cette section: Lien
15.1 Packages et fonctions
| Analyse | Packages - Fonctions |
|---|---|
| Non paramétrique |
|
| Modèles à risques proportionnel |
|
| Modèles paramétriques (ph ou aft) |
|
| Risques concurents |
|
| Autres (graphiques - mise en forme) |
|
Pour les représentations graphiques, grâce aux infos et conseils de Nicolas Robette, je vais commencer à substituer les fonctions du package de survminer par celles du package ggsurvfit.
Dans un premier temps, cette mise à jour est effetuée pour les estimateurs de Kaplan Meier. Pour les risques concurrents, également pris en charge par ggsurvfit, il faudra également changer de package pour l’estimation, en utilisant tidycmprsk plutôt que le vieillissant cmprsk.
15.2 Analyse Non paramétrique
Chargement de la base transplantation
library(readr)
trans <- read.csv("https://raw.githubusercontent.com/mthevenin/analyse_duree/master/bases/transplantation.csv")15.2.1 Méthode actuarielle
La fonction disponible du paquet discsurv, lifetable(), a des fonctionalités plutôt limitées. Si on peut maintenant définir des intervalles de durée, il n’y a toujours pas d’estimateurs les différents quantiles de la courbe de survie, ce qui limite fortement sont utilisation.
La programmation est rendue un peu compliquée pour pas grand chose. Je donne les codes pour information, sans plus de commentaires.
trans = as.data.frame(trans)Fonction lifeTable
Intervalle par defaut \(dt=1\)
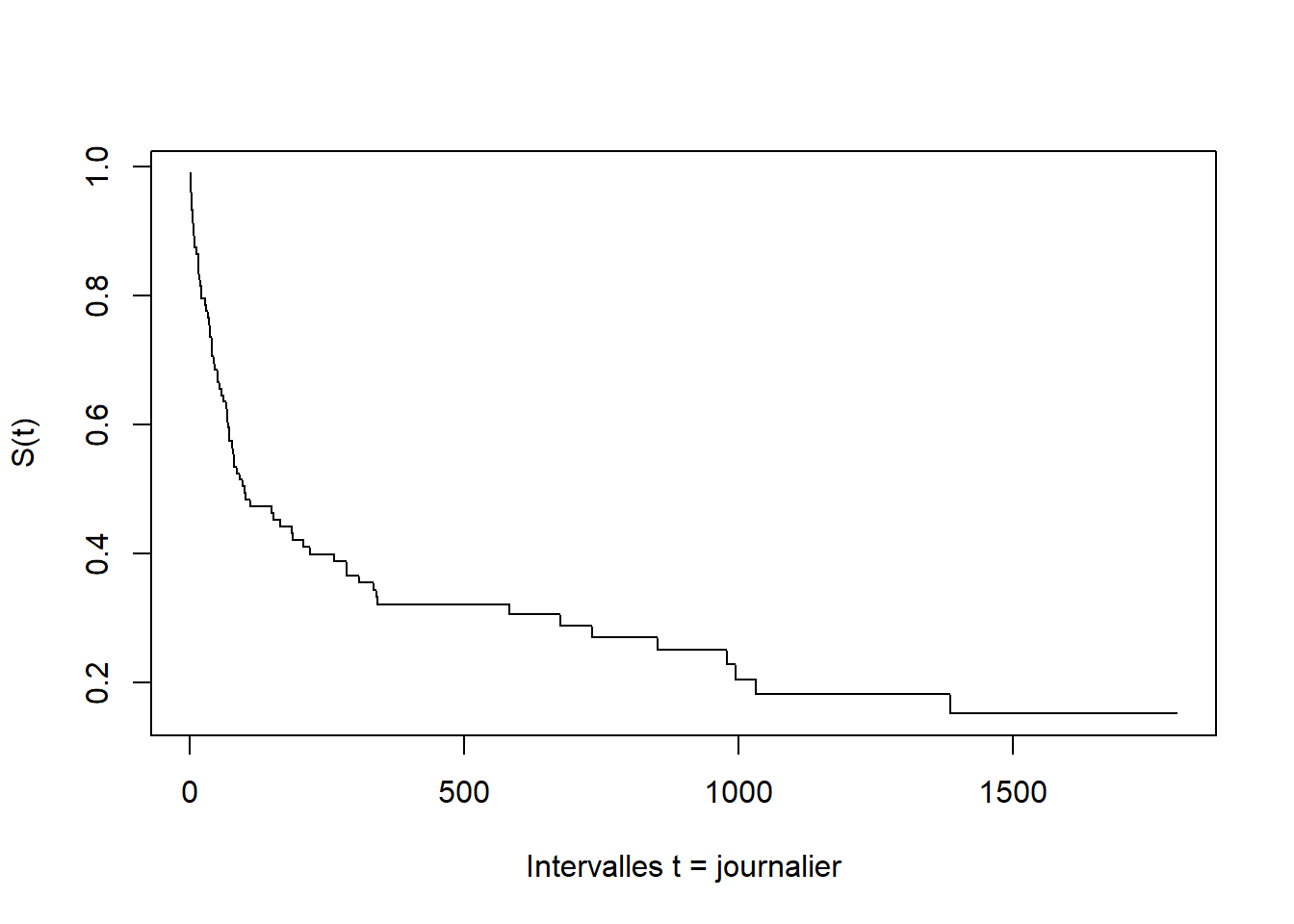
lt = lifeTable(dataShort=trans, timeColumn="stime", eventColumn = "died")
plot(lt, x = 1:dim(lt$Output)[1], y = lt$Output$S, xlab = "Intervalles t = journalier", ylab="S(t)")Intervalle \(dt=30\)
# On définit un vecteur définissant les intervalles (il n'y avait pas plus simple????)
dt <- 1:ceiling(max(trans$stime)/30)*30
# Base dis avec une nouvelle variable de durée => timeDisc
dis <- contToDisc(dataShort=trans, timeColumn="stime", intervalLimits = dt )
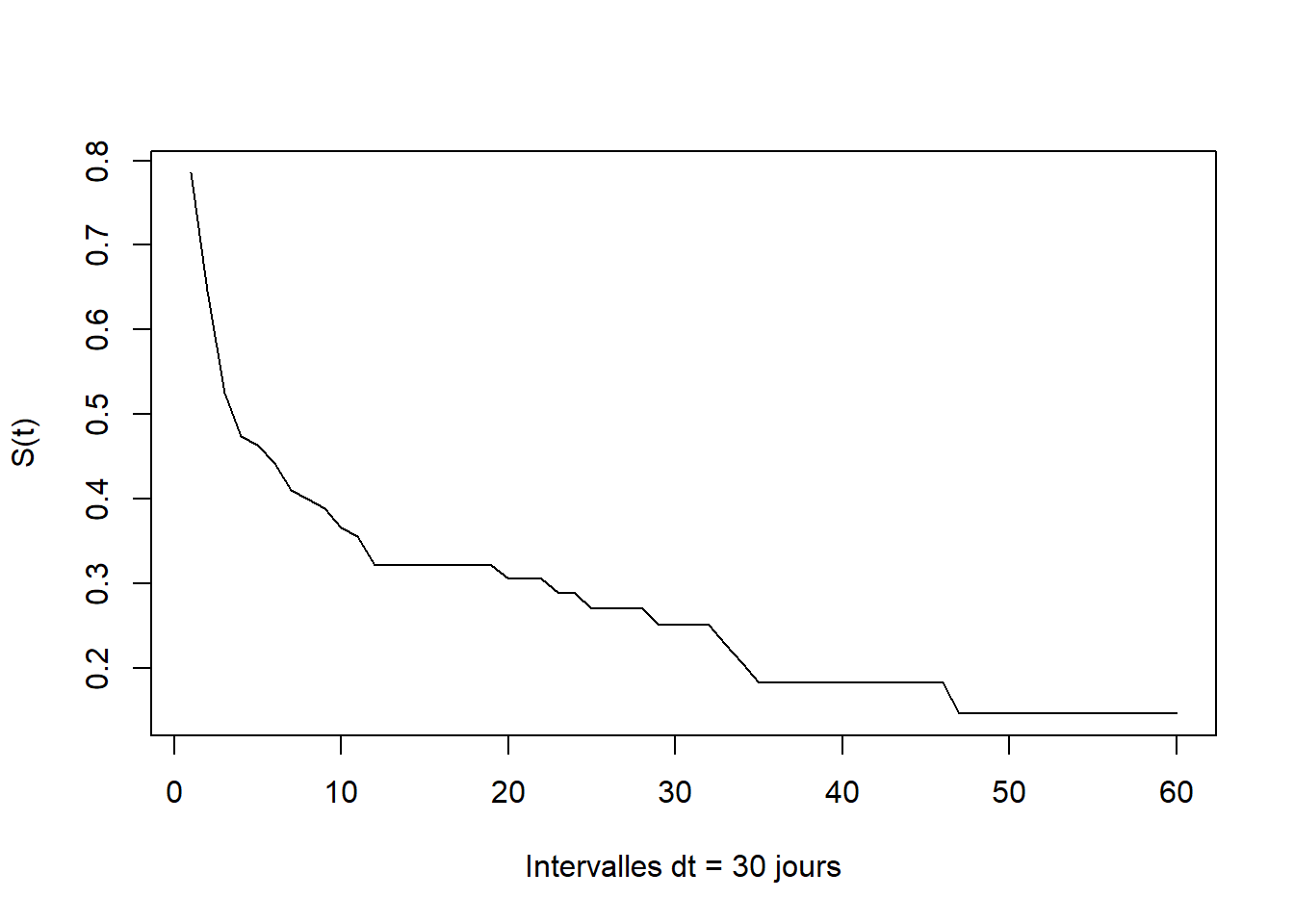
lt <- lifeTable(dataShort=dis, timeColumn="timeDisc", eventColumn = "died")
plot(lt, x = 1:dim(lt$Output)[1], y = lt$Output$S, xlab = "Intervalles dt = 30 jours", ylab="S(t)")Sur les abscisses, ce sont les valeurs des intervalles qui sont reportés: 10=300 jours. Ce n’est vraiment pas terrible. Pour ce type d’estimateurs, il est donc préférable d’utiliser Stata (ou Sas .
15.2.2 Méthode Kaplan-Meier
Le package survival est le principal outil d’analyse des durée. Le package survminer permet d’améliorer grandement la présentation des graphiques.
Estimation des fonctions de survie
Fonction survfit
Syntaxe
fit <- survfit(Surv(time, status) ~ x, data = nom_base)On peut renseigner directement les variables permettant de calculer la durée et non la variable de durée elle-même. Cette méthode est utilisée lorsqu’on introduit une variable dynamique dans un modèle semi-paramétrique de Cox (coxph).
Syntaxe
fit <- survfit(Surv(variable_start, variable_end, status) ~ x, data = nom_base)Sans comparaison de groupes:
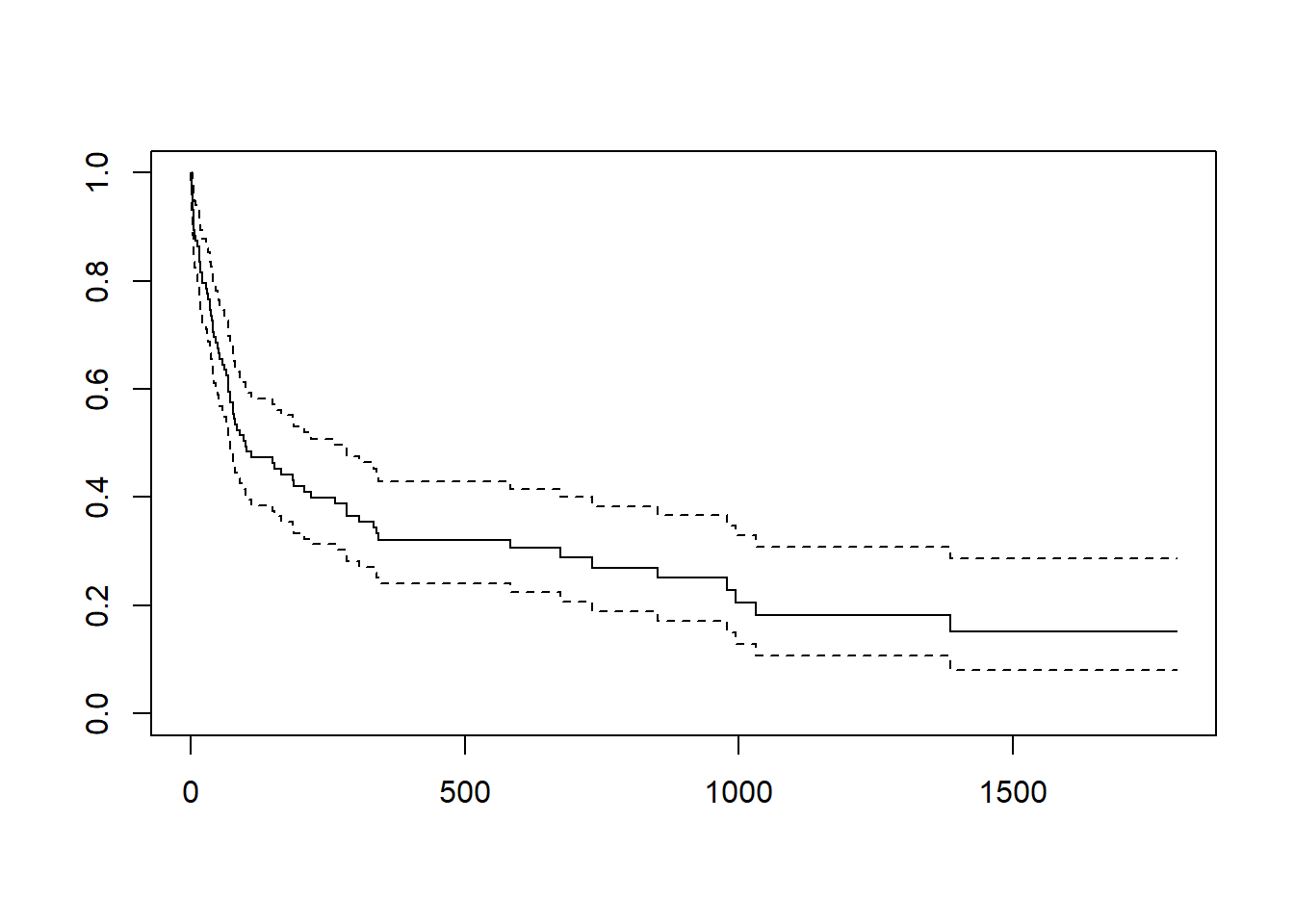
fit <- survfit(Surv(stime, died) ~ 1, data = trans)
fitCall: survfit(formula = Surv(stime, died) ~ 1, data = trans)
n events median 0.95LCL 0.95UCL
[1,] 103 75 100 72 263summary(fit)Call: survfit(formula = Surv(stime, died) ~ 1, data = trans)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 103 1 0.990 0.00966 0.9715 1.000
2 102 3 0.961 0.01904 0.9246 0.999
3 99 3 0.932 0.02480 0.8847 0.982
5 96 2 0.913 0.02782 0.8597 0.969
6 94 2 0.893 0.03043 0.8355 0.955
8 92 1 0.883 0.03161 0.8237 0.948
9 91 1 0.874 0.03272 0.8119 0.940
12 89 1 0.864 0.03379 0.8002 0.933
16 88 3 0.835 0.03667 0.7656 0.910
17 85 1 0.825 0.03753 0.7543 0.902
18 84 1 0.815 0.03835 0.7431 0.894
21 83 2 0.795 0.03986 0.7208 0.877
28 81 1 0.785 0.04056 0.7098 0.869
30 80 1 0.776 0.04122 0.6989 0.861
32 78 1 0.766 0.04188 0.6878 0.852
35 77 1 0.756 0.04250 0.6769 0.844
36 76 1 0.746 0.04308 0.6659 0.835
37 75 1 0.736 0.04364 0.6551 0.827
39 74 1 0.726 0.04417 0.6443 0.818
40 72 2 0.706 0.04519 0.6225 0.800
43 70 1 0.696 0.04565 0.6117 0.791
45 69 1 0.686 0.04609 0.6009 0.782
50 68 1 0.675 0.04650 0.5902 0.773
51 67 1 0.665 0.04689 0.5796 0.764
53 66 1 0.655 0.04725 0.5690 0.755
58 65 1 0.645 0.04759 0.5584 0.746
61 64 1 0.635 0.04790 0.5479 0.736
66 63 1 0.625 0.04819 0.5374 0.727
68 62 2 0.605 0.04870 0.5166 0.708
69 60 1 0.595 0.04892 0.5063 0.699
72 59 2 0.575 0.04929 0.4857 0.680
77 57 1 0.565 0.04945 0.4755 0.670
78 56 1 0.554 0.04958 0.4654 0.661
80 55 1 0.544 0.04970 0.4552 0.651
81 54 1 0.534 0.04979 0.4451 0.641
85 53 1 0.524 0.04986 0.4351 0.632
90 52 1 0.514 0.04991 0.4251 0.622
96 51 1 0.504 0.04994 0.4151 0.612
100 50 1 0.494 0.04995 0.4052 0.602
102 49 1 0.484 0.04993 0.3953 0.592
110 47 1 0.474 0.04992 0.3852 0.582
149 45 1 0.463 0.04991 0.3749 0.572
153 44 1 0.453 0.04987 0.3647 0.562
165 43 1 0.442 0.04981 0.3545 0.551
186 41 1 0.431 0.04975 0.3440 0.541
188 40 1 0.420 0.04966 0.3336 0.530
207 39 1 0.410 0.04954 0.3233 0.519
219 38 1 0.399 0.04940 0.3130 0.509
263 37 1 0.388 0.04923 0.3027 0.498
285 35 2 0.366 0.04885 0.2817 0.475
308 33 1 0.355 0.04861 0.2713 0.464
334 32 1 0.344 0.04834 0.2610 0.453
340 31 1 0.333 0.04804 0.2507 0.442
342 29 1 0.321 0.04773 0.2401 0.430
583 21 1 0.306 0.04785 0.2252 0.416
675 17 1 0.288 0.04830 0.2073 0.400
733 16 1 0.270 0.04852 0.1898 0.384
852 14 1 0.251 0.04873 0.1712 0.367
979 11 1 0.228 0.04934 0.1491 0.348
995 10 1 0.205 0.04939 0.1279 0.329
1032 9 1 0.182 0.04888 0.1078 0.308
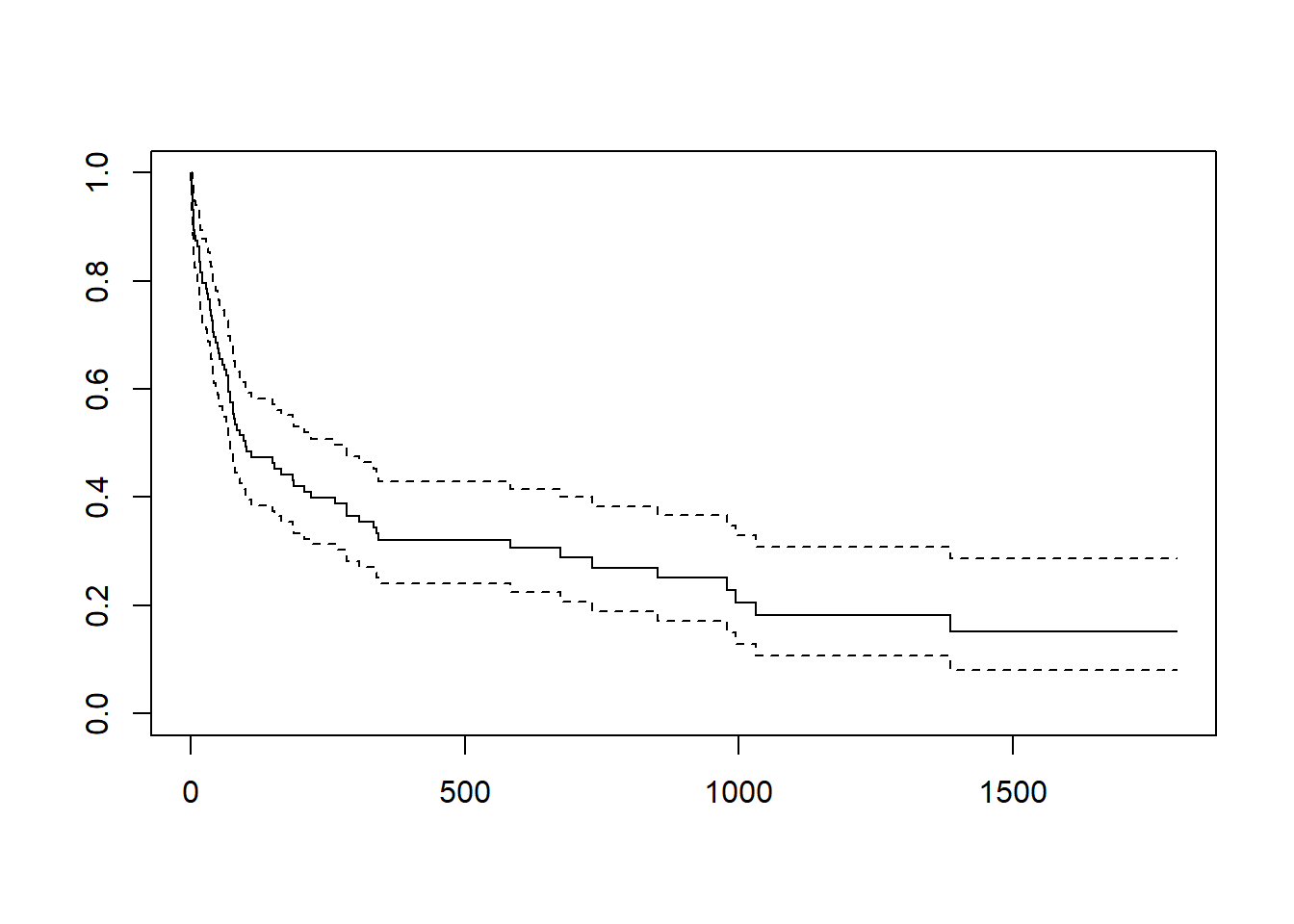
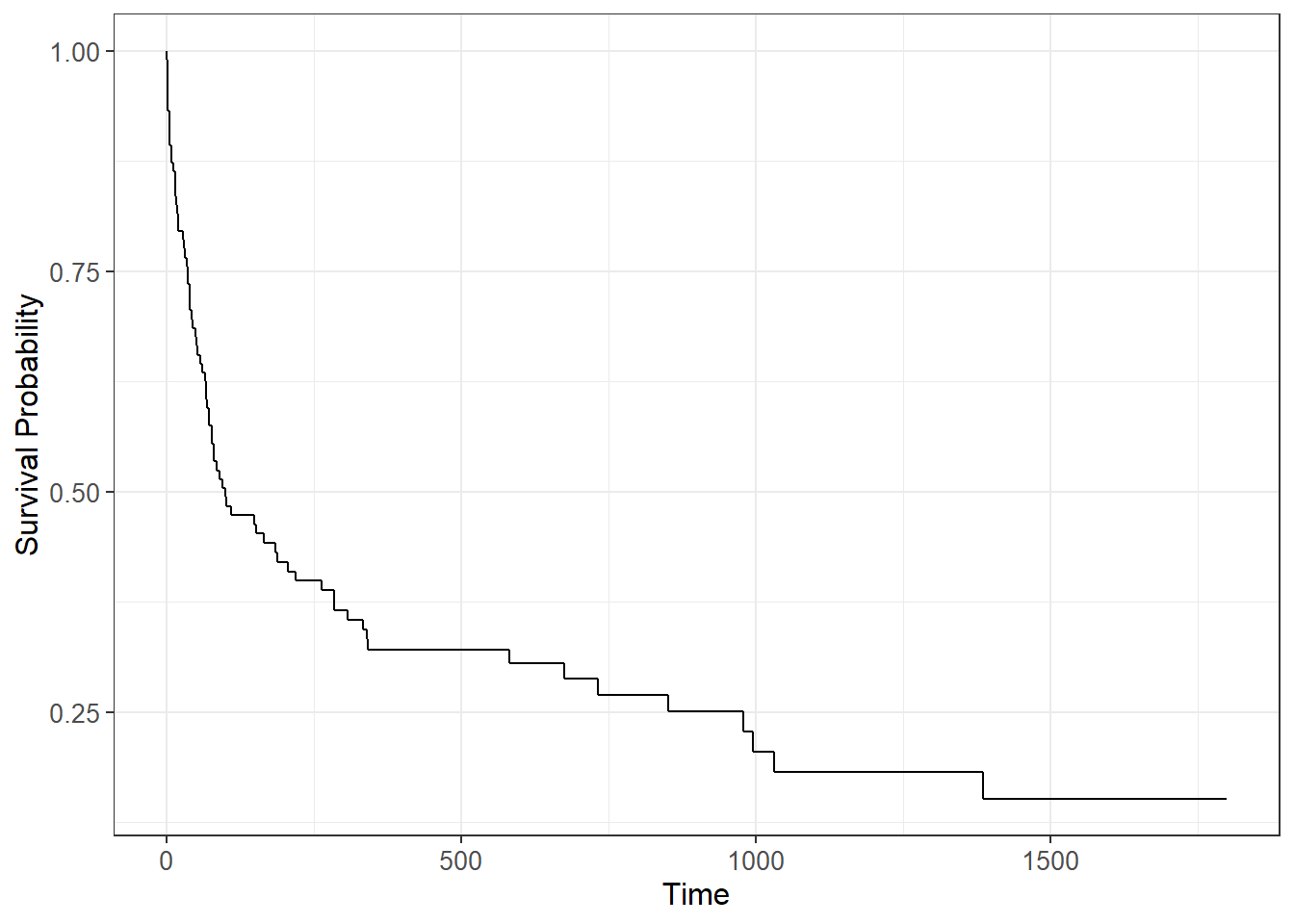
1386 6 1 0.152 0.04928 0.0804 0.287plot(fit)Le premier output fit permet d’obtenir la durée médiane, ici égale à 100 (\(S(100)=0.494\)). Le second avec la fonction summary permet d’obtenir une table des estimateurs. La fonction de survie peut être tracée avec la fonction plot (en pointillés les intervalles de confiance).
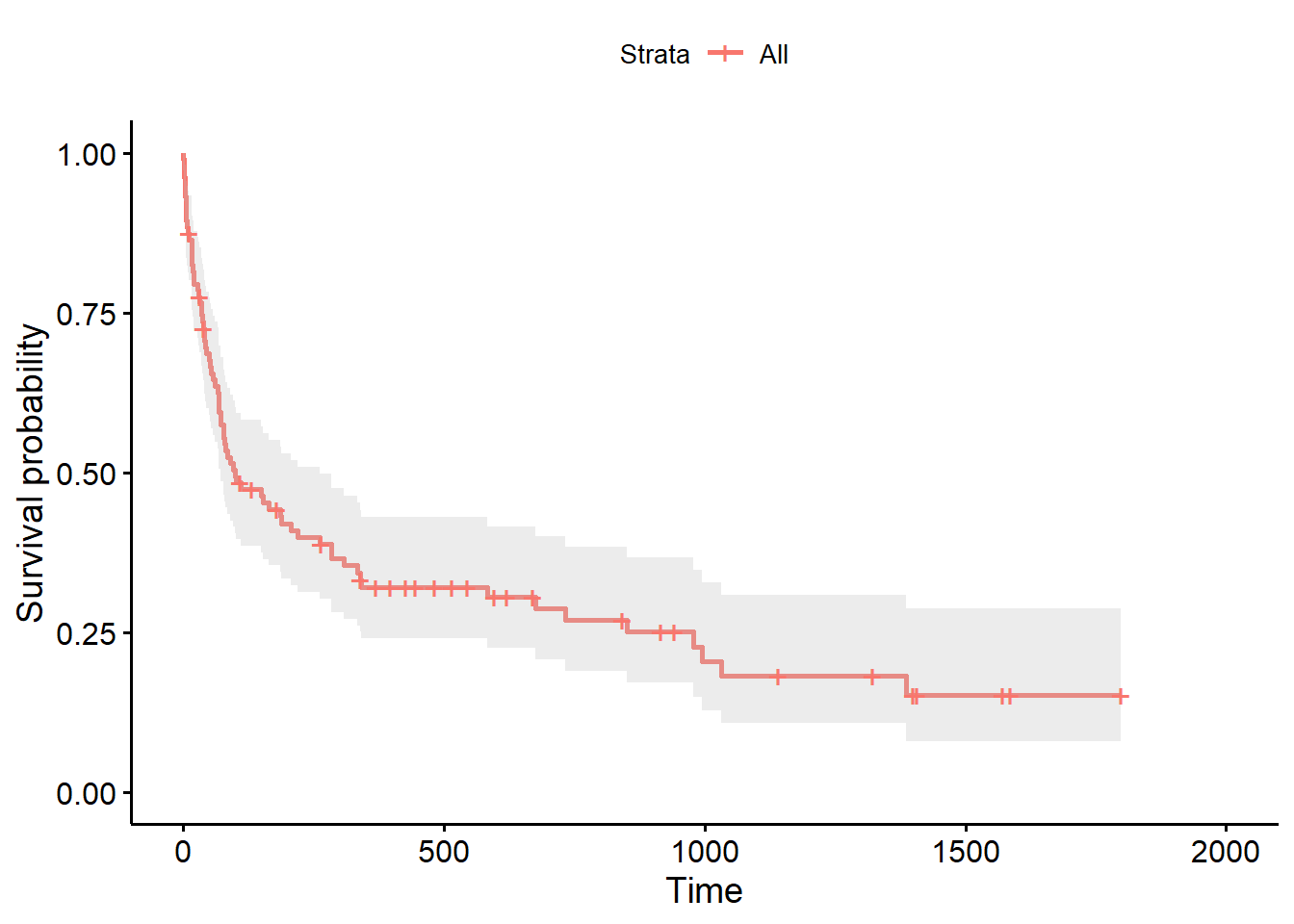
On peut obtenir des graphes demeilleur qualité avec le package ggsurvfit1
On peut ajouter la population encore soumise au risque à plusieurs points d’observation avec l’argument risk.table = TRUE, les intervalles de confiances.
15.2.3 Comparaison des S(t) méthode KM
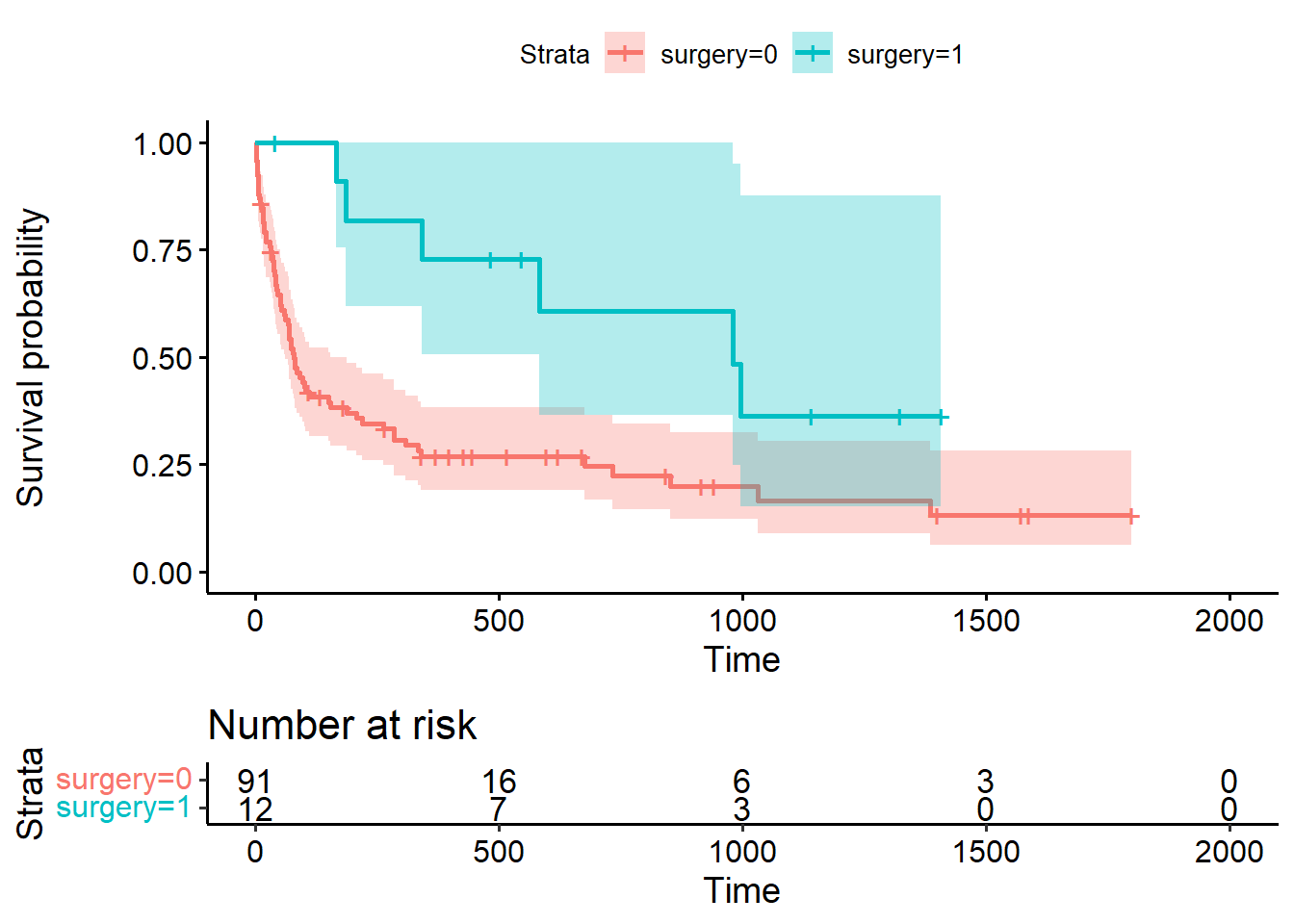
On va comparer les deux fonctions de séjour pour la variable surgery, celle pour les personnes non opérées et celle pour les personnes opérées.
fit <- survfit(Surv(stime, died) ~ surgery, data = trans)
fitCall: survfit(formula = Surv(stime, died) ~ surgery, data = trans)
n events median 0.95LCL 0.95UCL
surgery=0 91 69 78 61 153
surgery=1 12 6 979 583 NAggsurvfit(fit) +
add_confidence_interval() +
add_risktable()Tests du logrank
On utilise la fonction survdiff, avec comme variante le test des frères Peto (rho=1).
La syntaxe est quasiment identique à la fonction survdiff.
survdiff(Surv(stime, died) ~ surgery, rho=1, data = trans)Call:
survdiff(formula = Surv(stime, died) ~ surgery, data = trans,
rho = 1)
N Observed Expected (O-E)^2/E (O-E)^2/V
surgery=0 91 45.28 39.12 0.968 8.65
surgery=1 12 2.03 8.18 4.630 8.65
Chisq= 8.7 on 1 degrees of freedom, p= 0.003 Ici la variable est binaire. Si on veux tester deux à deux les niveaux d’une variable catégorielle à plus de deux modalités, il est fortement conseillé d’utiliser la fonction pairwise_survdiff de survminer (syntaxe identique que survdiff).
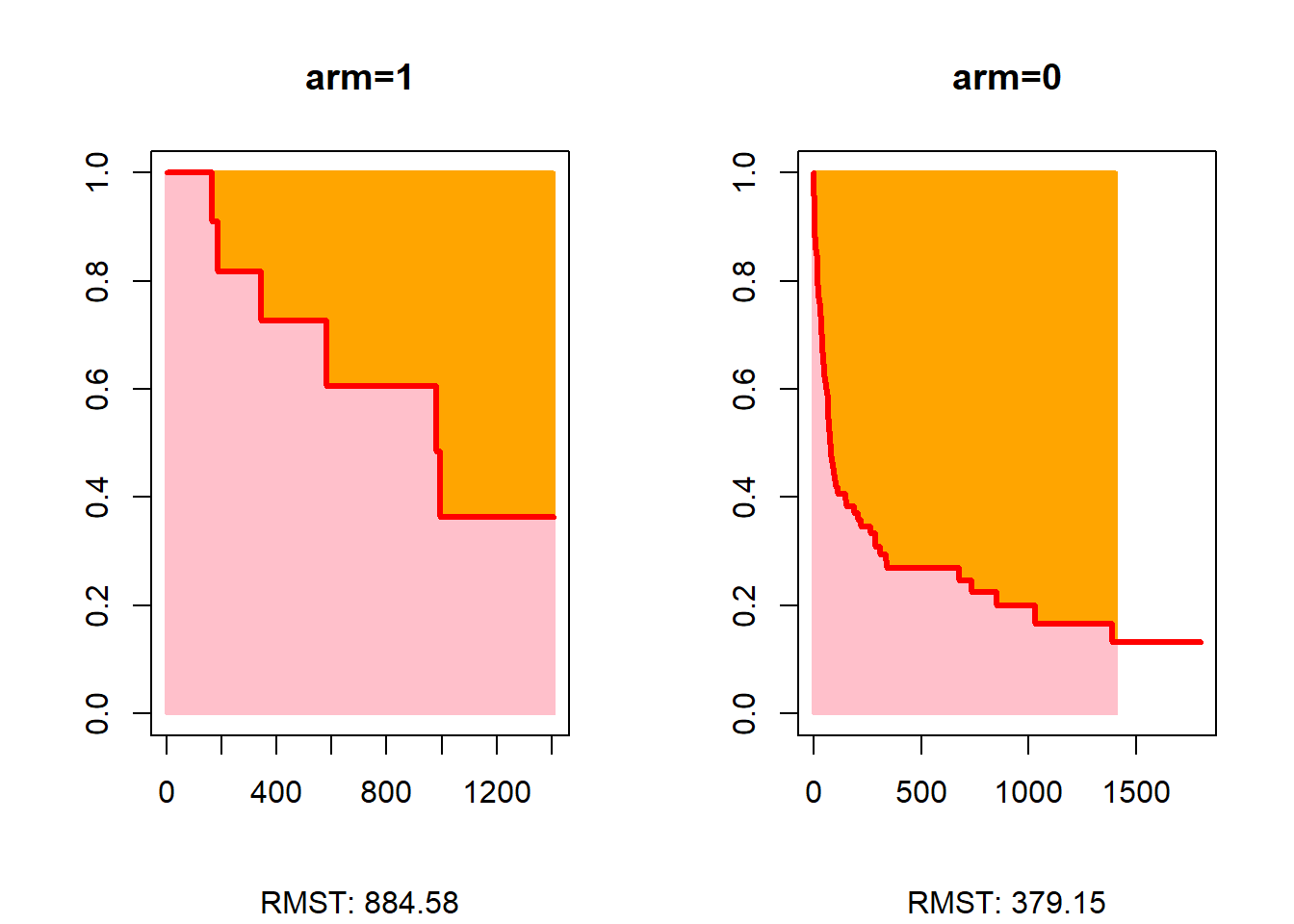
Comparaison des RMST
La fonction rmst2 du package survRM2 permet de comparer les RMST entre 2 groupes . La strate pour les comparaisons doit être impérativement renommée arm. La fonction, issue d’une commande de Stata, n’est pas très souple.
trans$arm=trans$surgery
a=rmst2(trans$stime, trans$died, trans$arm, tau=NULL)
print(a)
The truncation time, tau, was not specified. Thus, the default tau 1407 is used.
Restricted Mean Survival Time (RMST) by arm
Est. se lower .95 upper .95
RMST (arm=1) 884.576 151.979 586.702 1182.450
RMST (arm=0) 379.148 58.606 264.283 494.012
Restricted Mean Time Lost (RMTL) by arm
Est. se lower .95 upper .95
RMTL (arm=1) 522.424 151.979 224.550 820.298
RMTL (arm=0) 1027.852 58.606 912.988 1142.717
Between-group contrast
Est. lower .95 upper .95 p
RMST (arm=1)-(arm=0) 505.428 186.175 824.682 0.002
RMST (arm=1)/(arm=0) 2.333 1.483 3.670 0.000
RMTL (arm=1)/(arm=0) 0.508 0.284 0.909 0.022plot(a)15.3 Modèle de Cox
Ici tout est estimé, de nouveau, avec des fonctions du package survival:
- Estimation du modèle:
coxph. - Test de Grambsch-Therneau:
cox.zphetcox.oldzph. - Introduction d’une variable dynamique: allongement de la base avec
survsplit.
15.3.1 Estimation du modèle
Par défaut, R utilise la correction d’Efron pour les évènements simultanés. Il est préférable de ne pas la modifier.
Syntaxe:
Syntaxe
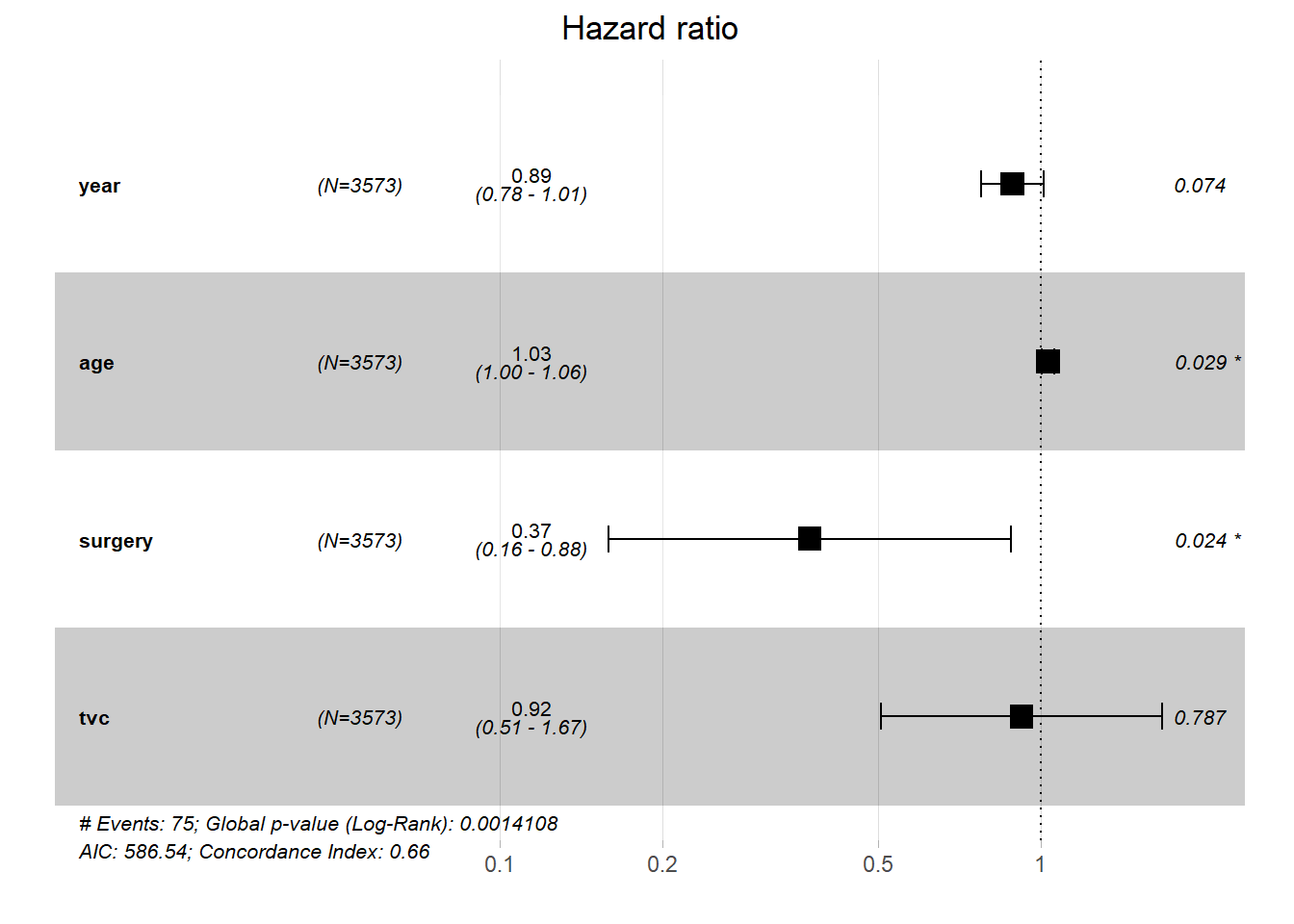
coxph(Surv(time, status) ~ x1 + x2 + ....., data=base, ties="nom_correction"))coxfit = coxph(formula = Surv(stime, died) ~ year + age + surgery, data = trans)
summary(coxfit)Call:
coxph(formula = Surv(stime, died) ~ year + age + surgery, data = trans)
n= 103, number of events= 75
coef exp(coef) se(coef) z Pr(>|z|)
year -0.11963 0.88725 0.06734 -1.776 0.0757
age 0.02958 1.03002 0.01352 2.187 0.0287
surgery -0.98732 0.37257 0.43626 -2.263 0.0236
exp(coef) exp(-coef) lower .95 upper .95
year 0.8872 1.1271 0.7775 1.0124
age 1.0300 0.9709 1.0031 1.0577
surgery 0.3726 2.6840 0.1584 0.8761
Concordance= 0.653 (se = 0.032 )
Likelihood ratio test= 17.63 on 3 df, p=5e-04
Wald test = 15.76 on 3 df, p=0.001
Score (logrank) test = 16.71 on 3 df, p=8e-04tbl_regression(coxfit, exponentiate = TRUE,)Registered S3 method overwritten by 'sass':
method from
print.css memiscCharacteristic |
HR 1 |
95% CI 1 |
p-value |
|---|---|---|---|
| year | 0.89 | 0.78, 1.01 | 0.076 |
| age | 1.03 | 1.00, 1.06 | 0.029 |
| surgery | 0.37 | 0.16, 0.88 | 0.024 |
| 1
HR = Hazard Ratio, CI = Confidence Interval |
|||
L’output des résultats reporte le logarithme des Risques Ratios (coef) ainsi que les RR (exp(coef)). Il est intéressant de regarder la valeur de concordance (Harrel’s) qui donne des indications sur la qualité de l’ajustement (proche de l’AUC/ROC d’un modèle probabiliste standard).
On peut représenter sous forme graphique les résultats avec la fonction ggforest de survminer
15.3.2 Hypothèse PH
15.3.2.1 Test Grambsch-Therneau
Résidus de Schoenfeld
Traditionnellement, on utilise la fonction cox.zph.
Depuis la v3 du package (2020), il permet d’effectuer le test original de Grambsch-Therneau qui repose sur le calcul exact des résidus. Malheureusement, celui ci pose de gros problèmes en présence de covariables corrélées, même faiblement. Situation classique dans les sciences sociales. Je ne déconseille fortement de l’utiliser. Il est donc préférable de rester sur le test reposant sur les moindres carrés ordinaires, implémenté jusqu’en 2023, et le seule disponible avec les autres outils: Stata, Python et Sas . On maintiendra donc une reproductibilité du test dans le temps et dans l’espace des logiciel.
Le test peut utiliser plusieurs transformation de la durée. Par défaut la fonction utilise \(1-KM\), soit le complémentaire de l’estimateur de Kaplan-Meier (option transform="km"). Cette expression complémentaire permet juste d’avoir une suite de valeur partant de 0 (la valeur de la fonction de survie partant par définition de 1).
Test GLS (v3 de survival)… WARNING
Avec transform="km"
cox.zph(coxfit) chisq df p
year 3.309 1 0.069
age 0.922 1 0.337
surgery 5.494 1 0.019
GLOBAL 8.581 3 0.035Avec transform="identity" (\(f(t)=t\))
cox.zph(coxfit, transform="identity") chisq df p
year 4.54 1 0.033
age 1.71 1 0.191
surgery 4.92 1 0.027
GLOBAL 9.47 3 0.024Remarque: avec la v3 de survival, quelques options ont été ajoutées tel que terms qui permet pour une variable catégorielle à plus de deux modalités de choisir entre un sous test multiple sur la variable (k modalités => k-1 degré de liberté) et une série de tests à 1 degré de liberté sur chaque modalité (k-1 tests). De mon point de vue préférer la seconde solution avec terms=FALSE. Le test de Grambsch-Therneau sous sa forme multiple étant particulièrement sensible au nombre de degrés de liberté, il est à mon sens préférable d’évaluer la proportionnalité variable par variable, donc degré de liberté par degré de liberté.
Test OLS (v2 de survival - Stata - Sas - Python)…Use it
Récupération du test ols
source("https://raw.githubusercontent.com/mthevenin/analyse_duree/main/cox.zphold/cox.zphold.R")Exécution du test ols
cox.zphold(coxfit, transform="identity")Warning in is.R(): 'is.R' est obsolète.
Voir help("Deprecated") et help("base-deprecated"). rho chisq p
year 0.102 0.797 0.3720
age 0.129 1.612 0.2043
surgery 0.297 5.539 0.0186
GLOBAL NA 8.756 0.0327On voit ici clairement que le test exact accentue la déviation vers la. C’est du tout simplement à la corrélation entre la variable surgery et la variable year. Les conclusions de S.Metzger sont ici bien vérifiées.
15.3.2.2 Introduction d’une intéraction
Lorsque la covariable n’est pas continue, elle doit être impérativement transformée en indicatrice 2. Penser à vérifier en amont que les résultats du modèle sont bien identiques avec le modèle estimé précédemment (ne pas oublier d’omettre le niveau en référence).
La variable d’intéraction est tt(nom_variable), la fonction de la durée (ici forme linéaire simple) est indiquée en option de la fonction: tt = function(x, t, ...) x*t.
coxfit2 = coxph(formula = Surv(stime, died) ~ year + age + surgery + tt(surgery),
data = trans, tt = function(x, t, ...) x*t)
summary(coxfit2)Call:
coxph(formula = Surv(stime, died) ~ year + age + surgery + tt(surgery),
data = trans, tt = function(x, t, ...) x * t)
n= 103, number of events= 75
coef exp(coef) se(coef) z Pr(>|z|)
year -0.123074 0.884198 0.066835 -1.841 0.06555 .
age 0.028888 1.029310 0.013449 2.148 0.03172 *
surgery -1.754738 0.172953 0.674391 -2.602 0.00927 **
tt(surgery) 0.002231 1.002234 0.001102 2.024 0.04299 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
year 0.8842 1.1310 0.77564 1.0080
age 1.0293 0.9715 1.00253 1.0568
surgery 0.1730 5.7819 0.04612 0.6486
tt(surgery) 1.0022 0.9978 1.00007 1.0044
Concordance= 0.656 (se = 0.032 )
Likelihood ratio test= 21.58 on 4 df, p=2e-04
Wald test = 16.99 on 4 df, p=0.002
Score (logrank) test = 19 on 4 df, p=8e-04tbl_regression(coxfit2, exponentiate = TRUE, estimate_fun = purrr::partial(style_ratio, digits = 3))Registered S3 method overwritten by 'sass':
method from
print.css memiscCharacteristic |
HR 1 |
95% CI 1 |
p-value |
|---|---|---|---|
| year | 0.884 | 0.776, 1.008 | 0.066 |
| age | 1.029 | 1.003, 1.057 | 0.032 |
| surgery | 0.173 | 0.046, 0.649 | 0.009 |
| tt(surgery) | 1.002 | 1.000, 1.004 | 0.043 |
| 1
HR = Hazard Ratio, CI = Confidence Interval |
|||
Rappel: le paramètre estimé pour tt(surgery) ne reporte pas un rapport de risques, mais un rapport de de deux rapports de risques. C’est bien une double différence sur l’échelle d’estimation (log).
15.3.3 Introduction d’une variable dynamique (binaire)
La dimension dynamique est ici le fait d’avoir été opéré pour une greffe du coeur.
Etape 1: créer un vecteur donnant les durées aux temps d’évènement.
Etape 2: appliquer ce vecteurs de points de coupure à la fonction
survsplit.Etape 3: modifier la variable transplant (ou créer une nouvelle) à l’aide de la variable wait qui prend la valeur 1 à partir du jour de la greffe, 0 avant.
Etape 1: création de l’objet cut (vecteur), qui récupère les moments où au moins un évènement est observé.
cut= unique(trans$stime[trans$died == 1])
cut [1] 1 2 3 5 6 8 9 12 16 17 18 21 28 30 32
[16] 35 36 37 39 40 43 45 50 51 53 58 61 66 68 69
[31] 72 77 78 80 81 85 90 96 100 102 110 149 153 165 186
[46] 188 207 219 263 285 308 334 340 342 583 675 733 852 979 995
[61] 1032 1386Etape 2: allonger la base aux durées d’évènement
tvc = survSplit(data = trans, cut = cut, end = "stime", start = "stime0", event = "died")
head(tvc, n=20 ) id year age surgery transplant wait mois compet arm stime0 stime died
1 15 68 53 0 0 0 1 1 0 0 1 1
2 43 70 43 0 0 0 1 1 0 0 1 0
3 43 70 43 0 0 0 1 1 0 1 2 1
4 61 71 52 0 0 0 1 1 0 0 1 0
5 61 71 52 0 0 0 1 1 0 1 2 1
6 75 72 52 0 0 0 1 1 0 0 1 0
7 75 72 52 0 0 0 1 1 0 1 2 1
8 6 68 54 0 0 0 1 2 0 0 1 0
9 6 68 54 0 0 0 1 2 0 1 2 0
10 6 68 54 0 0 0 1 2 0 2 3 1
11 42 70 36 0 0 0 1 1 0 0 1 0
12 42 70 36 0 0 0 1 1 0 1 2 0
13 42 70 36 0 0 0 1 1 0 2 3 1
14 54 71 47 0 0 0 1 1 0 0 1 0
15 54 71 47 0 0 0 1 1 0 1 2 0
16 54 71 47 0 0 0 1 1 0 2 3 1
17 38 70 41 0 1 5 1 1 0 0 1 0
18 38 70 41 0 1 5 1 1 0 1 2 0
19 38 70 41 0 1 5 1 1 0 2 3 0
20 38 70 41 0 1 5 1 1 0 3 5 1On vérifie qu’on obtient les même résultats avec le modèle sans tvc
coxph(formula = Surv(stime0, stime, died) ~ year + age + surgery, data = tvc)Call:
coxph(formula = Surv(stime0, stime, died) ~ year + age + surgery,
data = tvc)
coef exp(coef) se(coef) z p
year -0.11963 0.88725 0.06734 -1.776 0.0757
age 0.02958 1.03002 0.01352 2.187 0.0287
surgery -0.98732 0.37257 0.43626 -2.263 0.0236
Likelihood ratio test=17.63 on 3 df, p=0.0005243
n= 3573, number of events= 75 - Etape 3: on génère la variable dynamique de sorte que les personnes n’apparaissent pas greffés avant l’opération
tvc$tvc=ifelse(tvc$transplant==1 & tvc$wait<=tvc$stime,1,0)Estimation du modèle
En format long, on doit préciser dans la formule l’intervalle de durée avec les variables stime0 (le début) et stime (la fin).
tvcfit = coxph(formula = Surv(stime0, stime, died) ~ year + age + surgery + tvc, data = tvc)
summary(tvcfit)Call:
coxph(formula = Surv(stime0, stime, died) ~ year + age + surgery +
tvc, data = tvc)
n= 3573, number of events= 75
coef exp(coef) se(coef) z Pr(>|z|)
year -0.12032 0.88664 0.06734 -1.787 0.0740 .
age 0.03044 1.03091 0.01390 2.190 0.0285 *
surgery -0.98289 0.37423 0.43655 -2.251 0.0244 *
tvc -0.08221 0.92108 0.30484 -0.270 0.7874
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
year 0.8866 1.128 0.7770 1.0117
age 1.0309 0.970 1.0032 1.0594
surgery 0.3742 2.672 0.1591 0.8805
tvc 0.9211 1.086 0.5068 1.6741
Concordance= 0.659 (se = 0.032 )
Likelihood ratio test= 17.7 on 4 df, p=0.001
Wald test = 15.79 on 4 df, p=0.003
Score (logrank) test = 16.74 on 4 df, p=0.002tbl_regression(tvcfit, exponentiate = TRUE, estimate_fun = purrr::partial(style_ratio, digits = 3))Characteristic |
HR 1 |
95% CI 1 |
p-value |
|---|---|---|---|
| year | 0.887 | 0.777, 1.012 | 0.074 |
| age | 1.031 | 1.003, 1.059 | 0.029 |
| surgery | 0.374 | 0.159, 0.880 | 0.024 |
| tvc | 0.921 | 0.507, 1.674 | 0.8 |
| 1
HR = Hazard Ratio, CI = Confidence Interval |
|||
15.4 Modèles à durée discrète
Pour la durée, on va utiliser la variable mois (regroupement sur 30 jours de stime).
La fonction uncount du package tidyr permettra de splitter la base aux durées d’observation. C’est ici la principale différence avec le modèle de Cox qui est une estimation aux durées d’évènement
trans <- read.csv("https://raw.githubusercontent.com/mthevenin/analyse_duree/master/bases/transplantation.csv")La variable mois, va être supprimée avec uncount. Comme on en aura besoin plus loin pour générer proprement la variable évènement, on peut créer ici une variable mirroir.
trans$T = trans$moisdt = uncount(trans,mois)
dt = dt[order(dt$id),]head(dt,11) id year age died stime surgery transplant wait compet T
48 1 67 30 1 50 0 0 0 1 2
49 1 67 30 1 50 0 0 0 1 2
10 2 68 51 1 6 0 0 0 1 1
18 3 68 54 1 16 0 1 1 1 1
36 4 68 40 1 39 0 1 36 2 2
37 4 68 40 1 39 0 1 36 2 2
20 5 68 20 1 18 0 0 0 1 1
5 6 68 54 1 3 0 0 0 2 1
466 7 68 50 1 675 0 1 51 1 23
467 7 68 50 1 675 0 1 51 1 23
468 7 68 50 1 675 0 1 51 1 23On va générer une variable type compteur pour mesurer la durée à chaque point d’observation.
dt$x=1
dt$t = ave(dt$x,dt$id, FUN=cumsum)
head(dt, n=8) id year age died stime surgery transplant wait compet T x t
48 1 67 30 1 50 0 0 0 1 2 1 1
49 1 67 30 1 50 0 0 0 1 2 1 2
10 2 68 51 1 6 0 0 0 1 1 1 1
18 3 68 54 1 16 0 1 1 1 1 1 1
36 4 68 40 1 39 0 1 36 2 2 1 1
37 4 68 40 1 39 0 1 36 2 2 1 2
20 5 68 20 1 18 0 0 0 1 1 1 1
5 6 68 54 1 3 0 0 0 2 1 1 1Si un individu est décédé, died=1 est reporté sur toute les lignes (idem qu’avec la variable dynamique). On va modifier la variable tel que died=0 si t<T$.
dt = arrange(dt,id,t)
dt$died[dt$t<dt$T]=0
head(dt, n=8) id year age died stime surgery transplant wait compet T x t
1 1 67 30 0 50 0 0 0 1 2 1 1
2 1 67 30 1 50 0 0 0 1 2 1 2
3 2 68 51 1 6 0 0 0 1 1 1 1
4 3 68 54 1 16 0 1 1 1 1 1 1
5 4 68 40 0 39 0 1 36 2 2 1 1
6 4 68 40 1 39 0 1 36 2 2 1 2
7 5 68 20 1 18 0 0 0 1 1 1 1
8 6 68 54 1 3 0 0 0 2 1 1 115.4.1 \(f(t)\) quantitative
Avec un effet quadratique d’ordre 3 ^[Attention ici cela marche bien. Bien vérifier qu’il n’y a pas un problème d’overfitting, comme c’est le cas dans le TP.
On centre également les variables year et age sur leur valeur moyenne pour donner un sens à la constante
dt$t2=dt$t^2
dt$t3=dt$t^3
my = mean(dt$year)
dt$yearb = dt$year - my
ma = mean(dt$age)
dt$ageb = dt$age - ma
dtfit = glm(died ~ t + t2 + t3 + yearb + ageb + surgery, data=dt, family="binomial")
summ(dtfit, confint=TRUE, exp=TRUE)| Observations | 1127 |
| Dependent variable | died |
| Type | Generalized linear model |
| Family | binomial |
| Link | logit |
| χ²(6) | 90.69 |
| p | 0.00 |
| Pseudo-R² (Cragg-Uhler) | 0.20 |
| Pseudo-R² (McFadden) | 0.16 |
| AIC | 474.67 |
| BIC | 509.86 |
| exp(Est.) | 2.5% | 97.5% | z val. | p | |
|---|---|---|---|---|---|
| (Intercept) | 0.44 | 0.27 | 0.72 | -3.29 | 0.00 |
| t | 0.69 | 0.59 | 0.81 | -4.52 | 0.00 |
| t2 | 1.01 | 1.00 | 1.02 | 2.83 | 0.00 |
| t3 | 1.00 | 1.00 | 1.00 | -2.11 | 0.03 |
| yearb | 0.88 | 0.76 | 1.01 | -1.80 | 0.07 |
| ageb | 1.03 | 1.00 | 1.06 | 2.27 | 0.02 |
| surgery | 0.36 | 0.15 | 0.88 | -2.25 | 0.02 |
| Standard errors: MLE |
tbl_regression(dtfit, exponentiate = TRUE, estimate_fun = purrr::partial(style_ratio, digits = 3))Characteristic |
OR 1 |
95% CI 1 |
p-value |
|---|---|---|---|
| t | 0.689 | 0.582, 0.805 | <0.001 |
| t2 | 1.014 | 1.005, 1.025 | 0.005 |
| t3 | 1.000 | 1.000, 1.000 | 0.035 |
| yearb | 0.876 | 0.756, 1.011 | 0.072 |
| ageb | 1.034 | 1.006, 1.066 | 0.023 |
| surgery | 0.364 | 0.136, 0.815 | 0.024 |
| 1
OR = Odds Ratio, CI = Confidence Interval |
|||
15.4.2 \(f(t)\) en indicatrices
On va créer une variable de type discrète regroupant la variable t sur ses quartiles (pour l’exemple seulement, tous types de regroupement est envisageable).
On utilisera utiliser la fonction quantcut du package gtools.
dt$ct4 <- quantcut(dt$t)
table(dt$ct4)
[1,4] (4,11] (11,23] (23,60]
299 275 282 271 On va générer un compteur et un total d’observations sur la strate regroupant id et ct4.
dt$n = ave(dt$x,dt$id, dt$ct4, FUN=cumsum)
dt$N = ave(dt$x,dt$id, dt$ct4, FUN=sum)On conserve la dernière observation dans la strate.
dt2 = subset(dt, n==N)Estimation du modèle
fit = glm(died ~ ct4 + yearb + ageb + surgery, data=dt2, family=binomial)
summ(fit, confint=TRUE, exp=TRUE)| Observations | 197 |
| Dependent variable | died |
| Type | Generalized linear model |
| Family | binomial |
| Link | logit |
| χ²(6) | 39.30 |
| p | 0.00 |
| Pseudo-R² (Cragg-Uhler) | 0.25 |
| Pseudo-R² (McFadden) | 0.15 |
| AIC | 236.48 |
| BIC | 259.46 |
| exp(Est.) | 2.5% | 97.5% | z val. | p | |
|---|---|---|---|---|---|
| (Intercept) | 1.17 | 0.77 | 1.79 | 0.73 | 0.47 |
| ct4(4,11] | 0.36 | 0.16 | 0.81 | -2.47 | 0.01 |
| ct4(11,23] | 0.20 | 0.07 | 0.58 | -2.96 | 0.00 |
| ct4(23,60] | 0.62 | 0.19 | 2.01 | -0.80 | 0.42 |
| yearb | 0.82 | 0.68 | 0.98 | -2.18 | 0.03 |
| ageb | 1.05 | 1.01 | 1.09 | 2.53 | 0.01 |
| surgery | 0.33 | 0.12 | 0.88 | -2.21 | 0.03 |
| Standard errors: MLE |
tbl_regression(fit, exponentiate = TRUE, estimate_fun = purrr::partial(style_ratio, digits = 3))Characteristic |
OR 1 |
95% CI 1 |
p-value |
|---|---|---|---|
| ct4 | |||
| [1,4] | — | — | |
| (4,11] | 0.356 | 0.152, 0.792 | 0.014 |
| (11,23] | 0.199 | 0.061, 0.541 | 0.003 |
| (23,60] | 0.619 | 0.183, 1.981 | 0.4 |
| yearb | 0.816 | 0.677, 0.977 | 0.029 |
| ageb | 1.048 | 1.012, 1.089 | 0.011 |
| surgery | 0.330 | 0.113, 0.837 | 0.027 |
| 1
OR = Odds Ratio, CI = Confidence Interval |
|||
15.5 Modèles paramétriques usuels
Pour le modèle de Weibull par exemple.
- De type AFT
On utilise la fonction survreg du package survival
weibull = survreg(formula = Surv(stime, died) ~ year + age + surgery, data = trans, dist="weibull")
summary(weibull)
Call:
survreg(formula = Surv(stime, died) ~ year + age + surgery, data = trans,
dist = "weibull")
Value Std. Error z p
(Intercept) -3.0220 8.7284 -0.35 0.729
year 0.1620 0.1218 1.33 0.184
age -0.0615 0.0247 -2.49 0.013
surgery 1.9703 0.7794 2.53 0.011
Log(scale) 0.5868 0.0927 6.33 2.5e-10
Scale= 1.8
Weibull distribution
Loglik(model)= -488.2 Loglik(intercept only)= -497.6
Chisq= 18.87 on 3 degrees of freedom, p= 0.00029
Number of Newton-Raphson Iterations: 5
n= 103 tbl_regression(weibull, exponentiate = TRUE, estimate_fun = purrr::partial(style_ratio, digits = 3))Warning: The `exponentiate` argument is not supported in the `tidy()` method
for `survreg` objects and will be ignored.Characteristic |
exp(Beta) |
95% CI 1 |
p-value |
|---|---|---|---|
| year | 0.162 | -0.077, 0.401 | 0.2 |
| age | -0.062 | -0.110, -0.013 | 0.013 |
| surgery | 1.970 | 0.443, 3.498 | 0.011 |
| 1
CI = Confidence Interval |
|||
- De type PH
La paramétrisation PH n’est pas possible avec la fonction survreg. Il faut utiliser le package flexsurv, qui permet également d’estimer les modèles paramétriques disponibles avec survival. La syntaxe est quasiment identique.
Pour estimer le modèle de Weibull de type PH, on utilise en option l’agument dist="weibullPH.
weibullph = flexsurvreg(formula = Surv(stime, died) ~ year + age + surgery, data = trans, dist="weibullPH")
weibullphCall:
flexsurvreg(formula = Surv(stime, died) ~ year + age + surgery,
data = trans, dist = "weibullPH")
Estimates:
data mean est L95% U95% se exp(est)
shape NA 5.56e-01 4.64e-01 6.67e-01 5.16e-02 NA
scale NA 5.37e+00 4.21e-04 6.85e+04 2.59e+01 NA
year 7.06e+01 -9.01e-02 -2.20e-01 4.00e-02 6.64e-02 9.14e-01
age 4.46e+01 3.42e-02 7.11e-03 6.13e-02 1.38e-02 1.03e+00
surgery 1.17e-01 -1.10e+00 -1.95e+00 -2.45e-01 4.34e-01 3.34e-01
L95% U95%
shape NA NA
scale NA NA
year 8.02e-01 1.04e+00
age 1.01e+00 1.06e+00
surgery 1.43e-01 7.83e-01
N = 103, Events: 75, Censored: 28
Total time at risk: 31938
Log-likelihood = -488.1683, df = 5
AIC = 986.336615.6 Risques concurrents
Mise à jour des packages prévues pour la fin de l’année:
cmprsk=>tidycmprsksurvminer=>ggsurvfit
Le package cmprsk pour l’analyse non paramétrique et le modèle de Fine-Gray (non traité).
Package cmprsk pour l’analyse non paramétrique et le modèle de Fine-Gray. La variable de censure/évènement, compet, correspond à la variable died avec une modalité supplémentaire simulée. On suppose l’existence d’une cause supplémentaire au décès autre qu’une malformation cardiaque et non strictement indépendante de cell-ci.
compet <- read.csv("https://raw.githubusercontent.com/mthevenin/analyse_duree/master/bases/transplantation.csv")
# variable compet
table(compet$compet)
0 1 2
28 56 19 # variable died
table(compet$died)
0 1
28 75 15.6.0.1 Incidences cumulées
On utilise la fonction cuminc du package cmprsk.
Pas de comparaison de groupes
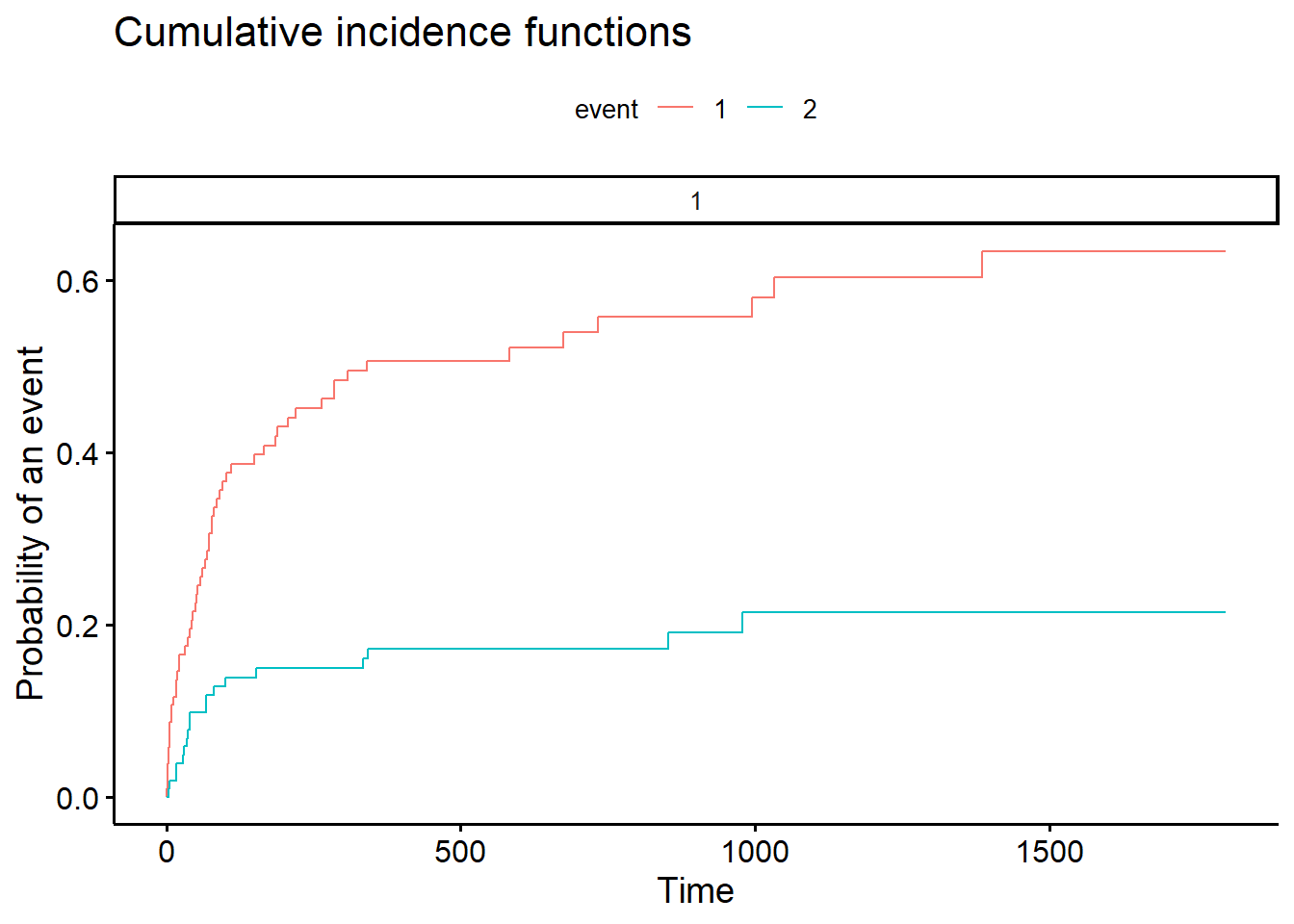
ic = cuminc(compet$stime, compet$compet)
ic Estimates and Variances:
$est
500 1000 1500
1 1 0.5067598 0.5808345 0.6340038
1 2 0.1720161 0.2140841 0.2140841
$var
500 1000 1500
1 1 0.002619449 0.003131847 0.003676516
1 2 0.001473283 0.002203770 0.002203770plot(ic)Avec survminer
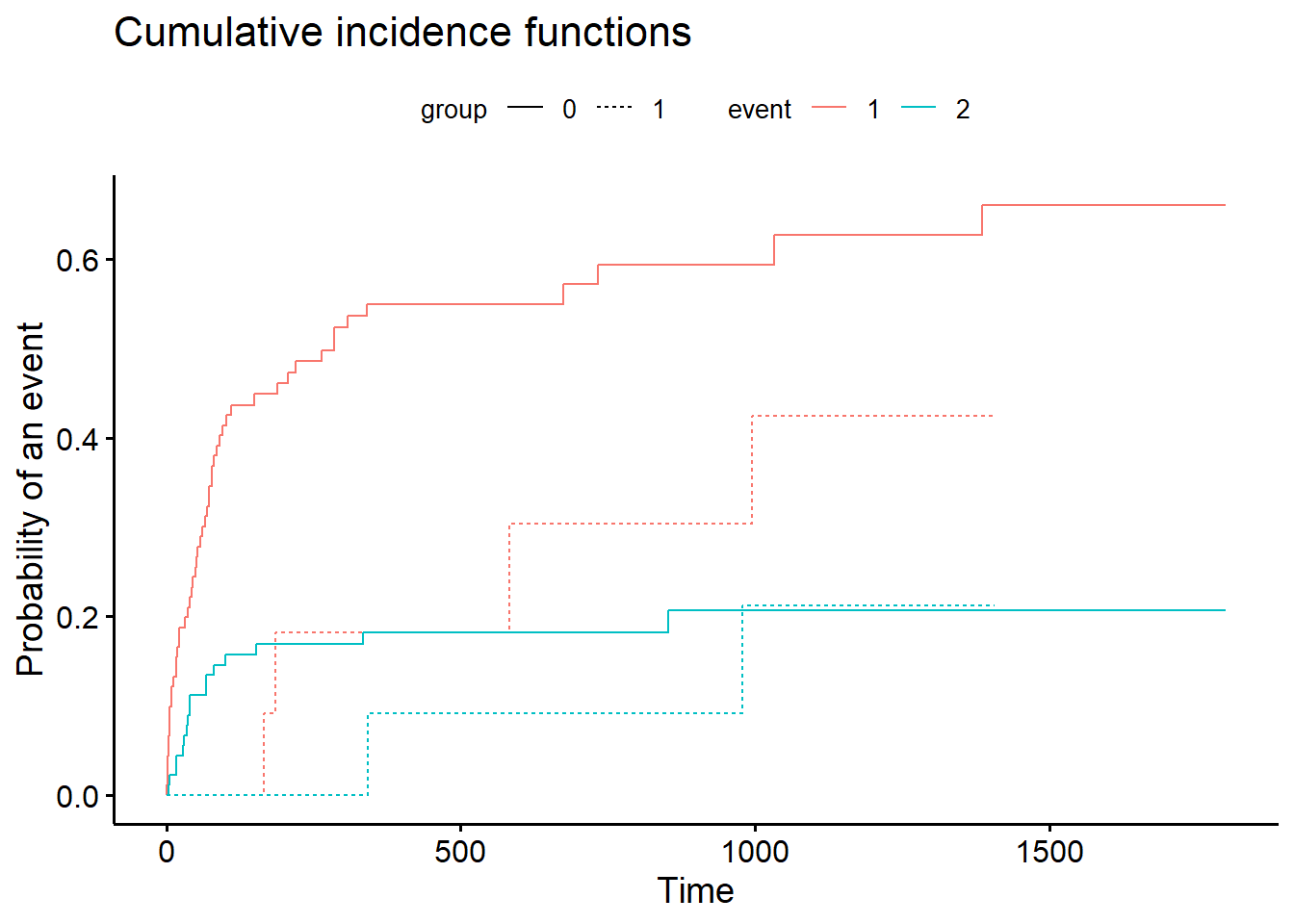
Comparaison de groupes
Le test de Gray est automatiquement exécuté.
ic = cuminc(compet$stime, compet$compet, group=compet$surgery, rho=1)
ic Tests:
stat pv df
1 4.604792 0.03188272 1
2 0.272147 0.60189515 1
Estimates and Variances:
$est
500 1000 1500
0 1 0.54917896 0.5940358 0.6604903
1 1 0.18181818 0.4242424 NA
0 2 0.18168014 0.2066006 0.2066006
1 2 0.09090909 0.2121212 NA
$var
500 1000 1500
0 1 0.002955869 0.003335897 0.004199157
1 1 0.014958678 0.033339569 NA
0 2 0.001727112 0.002271242 0.002271242
1 2 0.008449138 0.022024737 NAplot(ic)Avec survminer, pour obtenir un seul graphique pour toutes les courbes ajouter l’option multiple_panels = F
15.6.0.2 Modèles
On va utilisé seulement le modèle multinomial à durée discrète, le modèle fine-gray pendant du modèle de Cox pour les risques concurrents étant fortement critiqué. Si une analyse de type cause-specific est envisageable (issues concurrentes traitées comme des censures à droites) on utilise simplement la fonction coxph de survival.
On va de nouveau utiliser la variable mois (durée discrète). Le modèle sera estimé à l’aide la fonction multinom du très vieillissant package nnet, les p-values doivent-être programmées, l’output ne donnant que les erreurs-types.
Mise en forme de la base
compet <- read.csv("https://raw.githubusercontent.com/mthevenin/analyse_duree/master/bases/transplantation.csv")
compet$T = compet$mois
td = uncount(compet, mois)
td = arrange(td, id)
td$x=1
td$t = ave(td$x, td$id, FUN=cumsum)
td$t2 = td$t^2
my = mean(td$year)
td$yearb = td$year - my
ma = mean(td$age)
td$ageb = td$age - ma
td$e = ifelse(td$t<td$T,0, td$compet)Estimation
Pour estimer le modèle, on utilise la fonction mlogit. Les p-values seront calculées à partir d’un test bilatéral (statistique z).
competfit = multinom(formula = e ~ t + t2 + yearb + ageb + surgery, data = td)# weights: 21 (12 variable)
initial value 1238.136049
iter 10 value 608.949443
iter 20 value 341.102661
iter 30 value 277.143136
iter 40 value 275.005451
final value 275.005419
convergedtbl_regression(competfit, exponentiate = TRUE,)Characteristic |
OR 1 |
95% CI 1 |
p-value |
|---|---|---|---|
| 1 | |||
| t | 0.82 | 0.75, 0.88 | <0.001 |
| t2 | 1.00 | 1.00, 1.00 | <0.001 |
| yearb | 0.88 | 0.75, 1.03 | 0.12 |
| ageb | 1.04 | 1.01, 1.08 | 0.012 |
| surgery | 0.32 | 0.11, 0.91 | 0.033 |
| 2 | |||
| t | 0.82 | 0.71, 0.94 | 0.003 |
| t2 | 1.00 | 1.00, 1.01 | 0.052 |
| yearb | 0.82 | 0.62, 1.07 | 0.14 |
| ageb | 1.01 | 0.96, 1.06 | 0.7 |
| surgery | 0.54 | 0.12, 2.50 | 0.4 |
| 1
OR = Odds Ratio, CI = Confidence Interval |
|||