Les tests d’égalités des fonctions de survie entre différentes valeurs d’une covariable sont calculés à partir de la méthode de Kaplan Meier.
L’utilisation du test correspond à la nécessité de déterminer si une même distribution gouverne les évènements observés dans les différentes strates.
Attention: pas de test possible sur des variables quantitatives. Il faut donc prévoir des regroupements pour les transformer en variable ordinale.
Deux méthodes sont utilisées:
La plus ancienne, la plus diffusée, et peut-être la moins bonne: test dits du log-rank).
Plus récente et (hélas) moins difusée: comparaison des RMST (Restricted Mean of Survival Time).
6.1 Tests du log-rank
Il s’agit d’une série de tests qui répondent à la même logique, la seule différence réside dans le poids accordé au début ou à la fin de la période d’observation. Par ailleurs ces différents tests sont plus ou moins sensibles à la distribution des censures à droites entre les sous échantillons et à la non proportionalité des risques.
Dans leur logique, ces tests entrent dans le cadre des tests d’indépendance du Khi2, même si formellement ils relèvent des techniques dites de rang.
Il s’agira donc de comparer des effectifs observés à des effectifs espérés à chaque moment d’évènement. La principale différence réside dans le calcul de la variance de la statistique du test qui, ici, suit assez logiquement une loi hypergéométrique [proche loi binomiale mais avec tirage avec remise].
6.1.1 Principe de calcul de la statistique de test
Effectifs observés en \(t_i\): \(o_{i1}\) et \(o_{i2}\) sont égaux à \(d_{i1}\) et \(d_{i2}\), et leur somme pour tous les temps d’évènement à \(O_1\) et \(O_2\).
Effectifs expérés (hypothèse nulle \(H_0\)): comme pour une statistique du \(\chi^2\) on se base sur les marges, avec le risque set (\(R_i\)) en \(t_i\) pour dénombrer les effectifs, soit \(e_{i1}=R_{i1}\times\frac{d_i}{R_i}\) et \(e_{i2}=R_{i2}\times\frac{d_2}{R_i}\). Leur somme pour tous les temps d’évènement est égale à \(E_1\) et \(E_2\). Le principe de calcul des effectifs observés reposent donc sur l’hypothèse d’un rapport des risques toujours égal à 1 au cours du temps (hypothèse fondamentale de risques proportionnels).
Statistique du log-rank: \((O_1 - E_1) = -(O_2 - E_2)\).
Statistique de test: sous \(H_0\), \(\frac{(O_1 - E_1)^2}{\sum{v_i}}\), avec \(v_i\) la variance de \((o_{i1} - e_{i2})\), suis un \(\chi^2(1)\). Si on teste simultanément la différence de \(g\) fonctions de survie, ce qui n’est pas une bonne idée en passant, la statistique de test suis un \(\chi^2(g-1)\).
6.1.2 Les principaux tests log-rank
Le principe de construction des effectifs observés et espérés reste le même dans chaque test, les différences résident dans les pondérations (\(w_i\)) qui prennent en compte, de manière différente, la taille de la population soumise au risque à chaque durée où au moins un évènement est observé.
Test du log-rank: \(w_i=1\)
Il accorde le même poids à toutes les durées d’évènement. C’est le test standard, le plus utilisé.
Test de Wilconxon-Breslow-Grehan: \(w_i=R_i\)
Les écarts entre effectifs observés et espérés sont pondérés par la population soumise à risque en \(t_i\). Le test accorde plus de poids au début de la période analysée, et il est sensible aux différences de distributions entre les strates des observations censurées.
Test de Tarone-Ware: \(w_i=\sqrt{R_i}\)
Variante du test précédent, il atténue le poids accordé aux évènements au début de la période d’observation. Il est par ailleurs moins sensible au problème de la distribution des censures entre les strates.
Test de Peto-Peto : \(w_i=S_i\)
La pondération est une variante de la fonction de survie KM (avec \(R_i=R_i+1\)). Le test n’est pas sensible au problème de distribution des censures.
Test de Fleming-Harington: \(w_i=(S_i)^p\times(1-S_i)^{q}\) avec \(0\leq{p}\leq{1}\) Il permet de paramétrer le poids accordé au début où à la fin de temps d’observation. Si \(p=q=0\) on retrouve le test de base non pondéré.
En pratique/remarques:
Les tests du log-rank sont sensibles à l’hypothèse de risques proportionnels (voir modèle semi-paramétrique de Cox). En pratique si des courbes de séjours se croisent, il est fortement déconseillé de les utiliser. Cela ne signifie pas que si les courbes ne se croisent pas, l’hypothèse de proportionalité des risques est respectée : des rapports de risque peuvent au cours du temps s’intensifier, se réduire ou, le cas échant s’inverser, ce qui est typique d’un croisement.
Effectuer un test global (multiple/omnibus) sur un nombre important de groupes (ou >2) peut rendre le test très facilement significatif. Il peut être intéressant de tester des courbes deux à deux (idem qu’une régression avec covariable discrète), en conservant un seul degré de liberté. Des méthodes de correction du test multiple sont possibles ou disponibles si on utilise R.
On utilise la fonction survdiff de la librairie survival. Le résultat du test de Peto-Peto est affiché par défaut (rho=1). Si on souhaite utiliser le test non pondéré, on ajoute l’option rho=0. Pour obtenir le résultat d’un test multiple corrigé (plus d’un degré de liberté), on peut utiliser la fonction pairwise_survdiff du package survminer. Cette fonction permet également d’obtenir des tests 2 à 2.
Je conseille de rester sur l’option Peto-Peto et dans le cas d’une variable à plus de deux modalités, d’utiliser la fonction de survminerpairwise_survdiff.
On utilise la commande sts test avec le nom de la version du test: peto, wilcoxon . Sans préciser le nom de la variante, le test non pondéré est exécuté.
Le test non pondéré et la version Wilcoxon sont données avec l’option strata de la proc lifetest. Attention : ne jamais utiliser la version LR Test qui est biaisée. Pour obtenir d’autres versions du test du log-rank, on ajoute /test=all à l’option strata.
Avec la librairie lifelines, on utilise la fonction logrank_test. Quatre variantes sont disponibles (Wilcoxon, Tarone-Ware, Peto-Peto et Fleming-Harrigton). On peut également utiliser la fonction duration.survdiff de statmodels (non pondéré, Wilcoxon - appelé ici Breslow- et Tarone-Ware).
6.1.3 Application
On compare ici l’effet du pontage coronarien sur le risque de décéder depuis l’inscription dans le registre de greffe.
Résultats des tests du logrank
Test
df
Chi2
P>Chi2
Non pondéré
1
6.59
0.0103
Wilcoxon (Breslow)
1
8.99
0.0027
Tarone-Ware
1
8.46
0.0036
Peto-Peto
8.66
0.0033
Les résultats font apparaître que l’opération permet d’augmenter la durée de survie des personnes. Il apparait que la p-value est plus élevée pour test non pondérée. Cela peut-il s’expliquer en regardant les deux courbes de séjours? Qu’en est-il de la proportionalité des risques ???? …. Réponse pendant la formation.
6.2 Comparaison des RMST
RMST: Restricted Mean of Survival Time
La comparaison des RMST est une alternative pertinente aux tests du log-rank car elle ne repose pas sur des hypothèses contraignantes (proportionnalité des risques, distribution des censures), et permet une lecture vivante basée sur des espérances de séjour et non sur la lecture d’une simple p-value traduisant l’homogénéité ou non des fonctions de séjour. Par ailleurs les comparaisons sont souples, on peut choisir un ou plusieurs points d’horizon pour alimenter l’analyse.
Principe
L’aire sous la fonction de survie représente la durée moyenne d’attente jusqu’à l’évènement, soit une espérance de survie.
En présence de censure à droite, il faut borner la durée maximale \(t^*<\infty\). L’espérance de survie s’interprète donc sur un horizon fini. On est très proche d’une mesure en analyse démographique type « espérance de vie partielle ».
\(RMST =\int_0^{t^*}S(t)dt\).
On peut facilement comparer les RMST de deux groupes, en termes de différence ou de ratio.
Par défaut on définit généralement \(t^*\) à partir le temps du dernier évènement observé. Il est néanmoins possible de calculer le RMST sur des intervalles plus court, ce qui lui permet une véritable souplesse au niveau de l’analyse.
R-Stata-Sas-Python
Attention, selon les logiciels la durée max par défaut n’est pas la même. Pour R et Sas, il s’agit du dernier évènement observé sur l’ensemble de l’échantillon, alors que Stata prend la durée qui correspond au dernier évènement observé le plus court des deux groupes . Cela affectera légèrement la valeur des Rmst estimées par défaut.
Pour l’exemple, la durée maximale utilisée par R est de 1407 jours alors que pour Stata elle est de 995 jours.
Librairie SurvRm2. Programmée par les mêmes personnes que la commande Stata, la fonction proposée n’est pas très souple.
Commande externe strmst2. La plus ancienne fonction proposée par les logiciels. Au final plus limitée que la solution Sas. J’ai programmé une commande, diffrmst, qui représente graphiquement les estimations des Rmst pour chaque temps d’évènement, leurs différences et les p-value issues des comparaisons.
Disponible depuis la version 15.1 de SAS/Stat (fin 2018). Les estimations et le résultat du test de comparaison sont récupérables très simplement dans une proc lifetest, avec en option **plots=(rmst)** . Bien que sortie tardivement par rapport Stata et R, les résultats sont particulièrement complets.
Estimation un peu pénible. A partir de l’estimateur KM obtenu avec la fonction KaplanMeierFitter de lifelines, on peut obtenir les RMST avec la fonction restricted_mean_survival_time. On peut tracer les fonctions, en revanche le test de comparaison n’est pas implémenté.
Application
Avec \(tmax=1407\):
Estimation des Rmst pour la variable surgery
Groupes
RMST
Std. Err
95% CI
\(surgery=1\)
884.576
187.263
517.546 - 1251.605
\(surgery=0\)
379.148
61.667
258.282 - 500.014
Différences entre Rmst pour la variable surgery
Types de contraste
Ecarts RMST
P>|z|
95% CI
\(Rmst(surgery1 - surgery0)\)
505.428
0.010
517.546 - 1251.605
\(Rmst\left(\frac{surgery1}{surgery0}\right)\)
2.333
0.002
1.383 - 3.937
Ici \(t^*\) est égal à 1407 jours, soit la durée qui correspond au dernier décès observé.
Sur un horizon de 1407 jours, ces individus opérés d’un pontage peuvent espérer vivre 884 jours en moyenne, contre 379 jours pour les autres. La durée moyenne de survie est donc 2.3 fois plus importante pour les personnes opérées (rapport des Rmst = 2.3 ), ce qui correspond à une différence de 379 jours.
Le tableau et le graphique suivant donnent les valeurs des Rmst et les écarts de la variable surgery en faisant varier \(tmax\) sur chaque jour où au moins un décès a été observé. Il a été réalisé avec Stata, la durée maximale utilisée a été paramétrée à 1407 jours (idem R, Sas).
Comme le premier décès observé pour les personnes opéré se situe le 165eme jours, il est tout à fait normal que pour ce groupe de personnes la valeur de la Rmst soit identique au jour de décès des individus non opérés.
Note
Pour la version pdf, seulement une dizaine de points a été sélectionné en raison de la longueur du tableau
Comparaison des Rmst à chaque jour où au moins un décès est observé
Code source
---#title: "**Tests de comparaison**"filters: - lightboxlightbox: auto---# **Tests de comparaison**- Les tests d'égalités des fonctions de survie entre différentes valeurs d'une covariable sont calculés à partir de la méthode de Kaplan Meier. - L'utilisation du test correspond à la nécessité de déterminer si une même distribution gouverne les évènements observés dans les différentes strates. - **Attention**: pas de test possible sur des variables quantitatives. Il faut donc prévoir des regroupements pour les transformer en variable ordinale. Deux méthodes sont utilisées: * La plus ancienne, la plus diffusée, et peut-être la moins bonne: test dits du **log-rank**). * Plus récente et (hélas) moins difusée: comparaison des **RMST** (*Restricted Mean of Survival Time*).## Tests du log-rankIl s'agit d'une série de tests qui répondent à la même logique, la seule différence réside dans le poids accordé au début ou à la fin de la période d'observation. Par ailleurs ces différents tests sont plus ou moins sensibles à la distribution des censures à droites entre les sous échantillons et à la non proportionalité des risques. Dans leur logique, ces tests entrent dans le cadre des tests d'indépendance du Khi2, même si formellement ils relèvent des techniques dites de rang. Il s'agira donc de comparer des effectifs observés à des effectifs espérés à chaque moment d'évènement. La principale différence réside dans le calcul de la variance de la statistique du test qui, ici, suit assez logiquement une loi hypergéométrique [proche loi binomiale mais avec tirage avec remise]. ### Principe de calcul de la statistique de test* **Effectifs observés en $t_i$**: $o_{i1}$ et $o_{i2}$ sont égaux à $d_{i1}$ et $d_{i2}$, et leur somme pour tous les temps d'évènement à $O_1$ et $O_2$.* **Effectifs expérés** (hypothèse nulle $H_0$): comme pour une statistique du $\chi^2$ on se base sur les marges, avec le risque set ($R_i$) en $t_i$ pour dénombrer les effectifs, soit $e_{i1}=R_{i1}\times\frac{d_i}{R_i}$ et $e_{i2}=R_{i2}\times\frac{d_2}{R_i}$. Leur somme pour tous les temps d'évènement est égale à $E_1$ et $E_2$. Le principe de calcul des effectifs observés reposent donc sur l'hypothèse d'un rapport des risques toujours égal à 1 au cours du temps (*hypothèse fondamentale de risques proportionnels*).* **Statistique du log-rank**: $(O_1 - E_1) = -(O_2 - E_2)$. * **Statistique de test**: sous $H_0$, $\frac{(O_1 - E_1)^2}{\sum{v_i}}$, avec $v_i$ la variance de $(o_{i1} - e_{i2})$, suis un $\chi^2(1)$.Si on teste simultanément la différence de $g$ fonctions de survie, ce qui n'est pas une bonne idée en passant, la statistique de test suis un $\chi^2(g-1)$. ### Les principaux tests log-rankLe principe de construction des effectifs observés et espérés reste le même dans chaque test, les différences résident dans les pondérations ($w_i$) qui prennent en compte, de manière différente, la taille de la population soumise au risque à chaque durée où au moins un évènement est observé. * **Test du log-rank**: $w_i=1$ Il accorde le même poids à toutes les durées d'évènement. C'est le test standard, le plus utilisé. * **Test de Wilconxon-Breslow-Grehan**: $w_i=R_i$ Les écarts entre effectifs observés et espérés sont pondérés par la population soumise à risque en $t_i$. Le test accorde plus de poids au début de la période analysée, et il est sensible aux différences de distributions entre les strates des observations censurées.* **Test de Tarone-Ware**: $w_i=\sqrt{R_i}$ Variante du test précédent, il atténue le poids accordé aux évènements au début de la période d'observation. Il est par ailleurs moins sensible au problème de la distribution des censures entre les strates. * **Test de Peto-Peto** : $w_i=S_i$ La pondération est une variante de la fonction de survie KM (avec $R_i=R_i+1$). Le test n'est pas sensible au problème de distribution des censures. * **Test de Fleming-Harington**: $w_i=(S_i)^p\times(1-S_i)^{q}$ avec $0\leq{p}\leq{1}$ Il permet de paramétrer le poids accordé au début où à la fin de temps d'observation. Si $p=q=0$ on retrouve le test de base non pondéré. **En pratique/remarques**: * Les tests du log-rank sont sensibles à l’hypothèse de risques proportionnels (voir **modèle semi-paramétrique de Cox**). En pratique si des courbes de séjours se croisent, il est fortement déconseillé de les utiliser. Cela ne signifie pas que si les courbes ne se croisent pas, l’hypothèse de proportionalité des risques est respectée : des rapports de risque peuvent au cours du temps s'intensifier, se réduire ou, le cas échant s’inverser, ce qui est typique d’un croisement.* Effectuer un test global (multiple/omnibus) sur un nombre important de groupes (ou >2) peut rendre le test très facilement significatif. Il peut être intéressant de tester des courbes deux à deux (idem qu’une régression avec covariable discrète), en conservant un seul degré de liberté. Des méthodes de correction du test multiple sont possibles ou disponibles si on utilise R. **R-Stata-Sas-Python** ::: panel-tabset#### R On utilise la fonction **`survdiff`** de la librairie `survival`. Le résultat du test de Peto-Peto est affiché par défaut (`rho=1`). Si on souhaite utiliser le test non pondéré, on ajoute l’option `rho=0`. Pour obtenir le résultat d'un test multiple corrigé (plus d’un degré de liberté), on peut utiliser la fonction **`pairwise_survdiff`** du package **`survminer`**. Cette fonction permet également d'obtenir des tests 2 à 2. Je conseille de rester sur l'option ***Peto-Peto*** et dans le cas d'une variable à plus de deux modalités, d'utiliser la fonction de `survminer` **`pairwise_survdiff`**.#### Stata On utilise la commande **`sts test`** avec le nom de la version du test: `peto`, `wilcoxon` . Sans préciser le nom de la variante, le test non pondéré est exécuté.#### SasLe test non pondéré et la version Wilcoxon sont données avec l’option **`strata`** de la `proc lifetest`. Attention : ne jamais utiliser la version *LR Test* qui est biaisée. Pour obtenir d’autres versions du test du log-rank, on ajoute **`/test=all`** à l’option `strata`.#### PythonAvec la librairie `lifelines`, on utilise la fonction **`logrank_test`**. Quatre variantes sont disponibles (Wilcoxon, Tarone-Ware, Peto-Peto et Fleming-Harrigton). On peut également utiliser la fonction **`duration.survdiff`** de `statmodels` (non pondéré, Wilcoxon - appelé ici Breslow- et Tarone-Ware). :::### Application On compare ici l'effet du pontage coronarien sur le risque de décéder depuis l'inscription dans le registre de greffe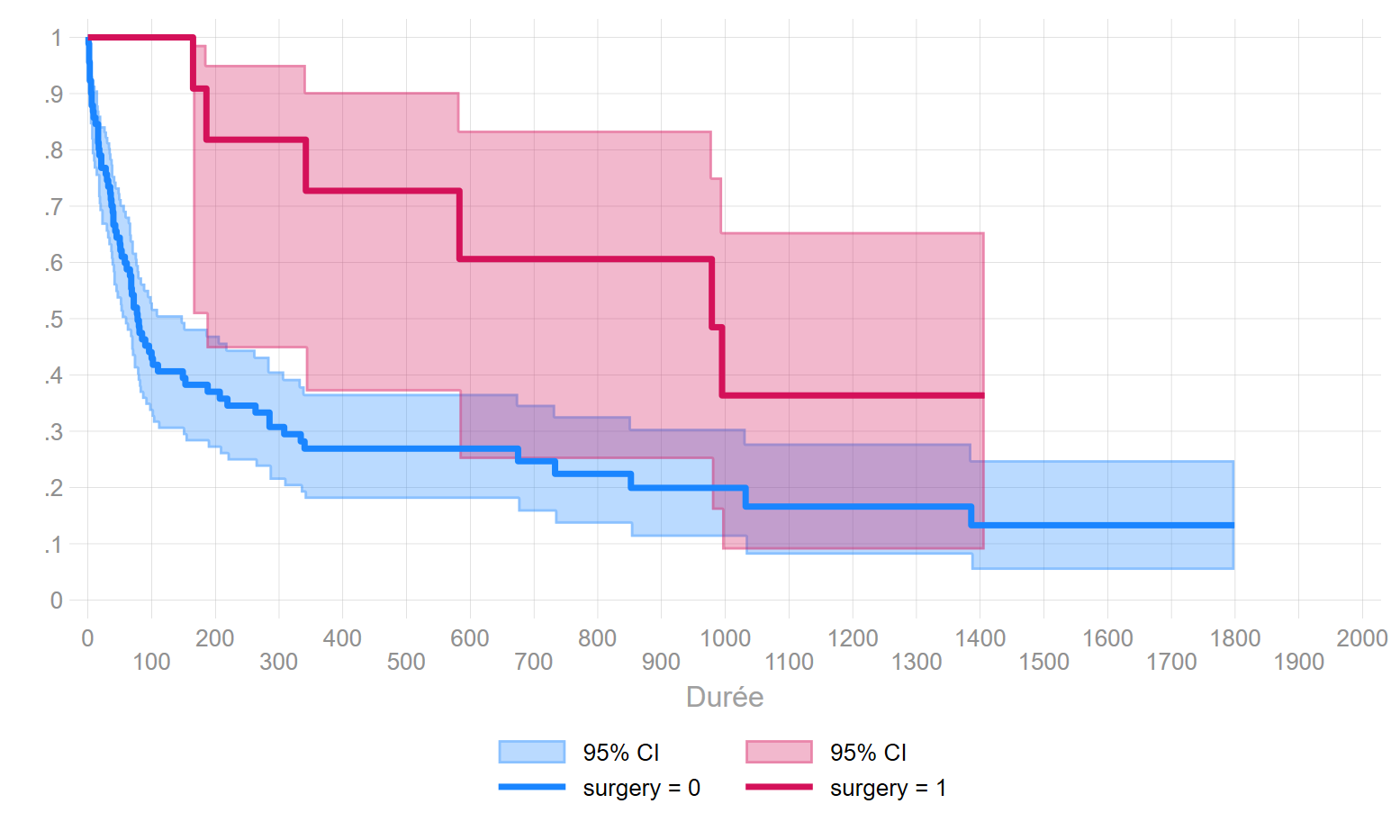. {width=70%}| **Test** | **df** | **Chi2** | **P>Chi2** ||------------------------|--------|----------|-------------|| **Non pondéré** | 1 | 6.59 | 0.0103 || **Wilcoxon (Breslow**) | 1 | 8.99 | 0.0027 || **Tarone-Ware** | 1 | 8.46 | 0.0036 || **Peto-Peto** | | 8.66 | 0.0033 |: Résultats des tests du logrankLes résultats font apparaître que l’opération permet d’augmenter la durée de survie des personnes. Il apparait que la p-value est plus élevée pour test non pondérée. Cela peut-il s'expliquer en regardant les deux courbes de séjours? Qu'en est-il de la proportionalité des risques ???? .... Réponse pendant la formation.## Comparaison des RMST **RMST**: *Restricted Mean of Survival Time* La comparaison des RMST est une alternative pertinente aux tests du log-rank car elle ne repose pas sur des hypothèses contraignantes (proportionnalité des risques, distribution des censures), et permet une lecture vivante basée sur des espérances de séjour et non sur la lecture d’une simple p-value traduisant l’homogénéité ou non des fonctions de séjour. Par ailleurs les comparaisons sont souples, on peut choisir un ou plusieurs points d’horizon pour alimenter l’analyse. **Principe** * L’aire sous la fonction de survie représente la durée moyenne d’attente jusqu'à l’évènement, soit une espérance de survie.* En présence de censure à droite, il faut borner la durée maximale $t^*<\infty$. L'espérance de survie s'interprète donc sur un horizon fini. On est très proche d’une mesure en analyse démographique type « espérance de vie partielle ».* $RMST =\int_0^{t^*}S(t)dt$. * On peut facilement comparer les RMST de deux groupes, en termes de différence ou de ratio. * Par défaut on définit généralement $t^*$ à partir le temps du dernier évènement observé. Il est néanmoins possible de calculer le RMST sur des intervalles plus court, ce qui lui permet une véritable souplesse au niveau de l’analyse. **R-Stata-Sas-Python** Attention, selon les logiciels la durée max par défaut n'est pas lamême. Pour R et Sas, il s'agit du dernier évènement observé sur l'ensemble de l'échantillon, alors que Stata prend la durée qui correspond au dernier évènement observé le plus court des deux groupes . Cela affectera légèrement la valeur des Rmst estimées par défaut. Pour l'exemple, la durée maximale utilisée par R est de 1407 jours alors que pour Stata elle est de 995 jours.::: panel-tabset#### R Librairie **`SurvRm2`**. Programmée par les mêmes personnes que la commande Stata, la fonction proposée n'est pas très souple.#### StataCommande externe **`strmst2`**. La plus ancienne fonction proposée par les logiciels. Au final plus limitée que la solution Sas. J’ai programmé une commande, `diffrmst`, qui représente graphiquement les estimations des Rmst pour chaque temps d’évènement, leurs différences et les p-value issues des comparaisons. #### SAS Disponible depuis la version 15.1 de SAS/Stat (fin 2018). Les estimations et le résultat du test de comparaison sont récupérables très simplement dans une `proc lifetest`, avec en option **`plots=(rmst)**` . Bien que sortie tardivement par rapport Stata et R, les résultats sont particulièrement complets.#### PythonEstimation un peu pénible. A partir de l'estimateur KM obtenu avec la fonction `KaplanMeierFitter` de `lifelines`, on peut obtenir les RMST avec la fonction `restricted_mean_survival_time`. On peut tracer les fonctions, en revanche le test de comparaison n'est pas implémenté.:::**Application** Avec $tmax=1407$:| Groupes | RMST | Std. Err | 95% CI ||-------------|---------|----------|--------------------|| $surgery=1$ | 884.576 | 187.263 | 517.546 - 1251.605 || $surgery=0$ | 379.148 | 61.667 | 258.282 - 500.014 |: Estimation des Rmst pour la variable surgery| Types de contraste | Ecarts RMST | P\>\|z\| | 95% CI ||----------------------------------------------|--------------|-----------|--------------------|| $Rmst(surgery1 - surgery0)$ | 505.428 | 0.010 | 517.546 - 1251.605 || $Rmst\left(\frac{surgery1}{surgery0}\right)$ | 2.333 | 0.002 | 1.383 - 3.937 |: Différences entre Rmst pour la variable surgeryIci $t^*$ est égal à 1407 jours, soit la durée qui correspond au dernier décès observé. Sur un horizon de 1407 jours, ces individus opérés d'un pontage peuvent espérer vivre 884 jours en moyenne, contre 379 jours pour les autres. La durée moyenne de survie est donc 2.3 fois plus importante pour les personnes opérées (rapport des Rmst = 2.3 ), ce qui correspond à une différence de 379 jours.Le tableau et le graphique suivant donnent les valeurs des Rmst et les écarts de la variable *surgery* en faisant varier $tmax$ sur chaque jour où au moins un décès a été observé. Il a été réalisé avec Stata, la durée maximale utilisée a été paramétrée à 1407 jours (idem R, Sas).Comme le premier décès observé pour les personnes opéré se situe le 165eme jours, il est tout à fait normal que pour ce groupe de personnes la valeur de la Rmst soit identique au jour de décès des individus non opérés.::: callout-notePour la version pdf, seulement une dizaine de points a été sélectionné en raison de la longueur du tableau:::::: {.content-visible when-format="html"}```{r eval=FALSE}#| code-fold: true#| code-summary: "**Afficher le tableau**"+--------------------------------------------------------------------------+| _time _rmst1 _rmst0 _diff 95%CI lower 95%CI upper pvalue||--------------------------------------------------------------------------||--------------------------------------------------------------------------||111000 . ||221.989011 .010989-.0104304 .0324084 .3146368||332.945055 .0549451-.0009099 .1108 .0538507||554.791209 .2087912 .0549289 .3626535 .0078217||665.692307 .3076923 .0995576 .5158269 .0037617||--------------------------------------------------------------------------||887.45055 .5494505 .2224352 .8764658 .0009908||998.318682 .6813186 .29139151.071246 .0006156||111110.03297 .9670329 .44614061.487925 .0002741||121210.890111.10989 .52126561.698514 .0002193||161614.274151.725846 .85885672.592834 .0000956||--------------------------------------------------------------------------||171715.086771.91323 .97697512.849484 .000062||181815.888252.1117451.105333.118161 .0000391||212118.259312.7406881.5162283.965148 .0000115||282823.635934.3640652.5987416.1293891.26e-06||303025.149854.850152.9247146.7755867.93e-07||--------------------------------------------------------------------------||313125.895685.1043243.0988627.1097876.08e-07||323226.64155.3584993.2722187.4447794.80e-07||353528.845086.1549233.8251028.4847442.24e-07||363629.56836.4316984.0204578.8429391.71e-07||373730.280236.7197744.2275459.2120041.26e-07||--------------------------------------------------------------------------||393931.681477.3185264.6641219.9729316.52e-08||404032.37087.6292024.89365310.364754.60e-08||434334.370978.6290345.65171911.606351.34e-08||454535.681819.3181896.17743512.458946.07e-09||505038.9024211.097587.53926114.65599.80e-10||--------------------------------------------------------------------------||515139.5352411.464767.82202815.107486.89e-10||535340.7782912.221718.41075616.032673.27e-10||585843.8293914.170619.93321618.4085.58e-11||616145.6261515.3738510.8772119.870492.07e-11||666648.5642517.4357512.5027522.368744.28e-12||--------------------------------------------------------------------------||686849.7168918.2831113.17523.391212.30e-12||696950.2706118.7293913.5362923.922481.56e-12||727251.8978720.1021314.6552625.549014.71e-13||777754.4969622.5030416.6375828.368515.51e-14||787855.0054722.9945317.0452828.943773.57e-14||--------------------------------------------------------------------------||808055.9999124.0000917.8850930.115091.44e-14||818156.4858224.5141818.3172230.711138.88e-15||858558.3842926.6157120.0920233.13941.33e-15||909060.7008729.2991322.3631136.235152.22e-16||969663.4129632.5870425.1503440.023730||--------------------------------------------------------------------------||10010065.1758334.8241827.0522942.596060||10210266.0346535.9653528.027443.903290||10910968.9614640.0385531.520348.556790||11011069.3795740.6204332.017649.223260||13113177.9160753.0839342.6726963.495170||--------------------------------------------------------------------------||14914985.2330763.7669351.7173575.816510||15315386.8112566.1887553.778178.59940||16516591.4023173.5976960.1188487.076550||180178.636497.1411381.4952366.4318896.558590||186184.090999.4366684.6542568.8452100.46330||--------------------------------------------------------------------------||188185.7273100.201885.5254469.46069101.59020||207201.2727107.236594.036275.10156112.97080||219211.0909111.531499.5595278.49335120.62570||263247.0909126.7362120.354790.2882150.42124.22e-15||265248.7273127.4026121.324690.82352151.82586.44e-15||--------------------------------------------------------------------------||285265.0909134.0671131.023896.0849165.96281.98e-13||308283.9091141.1416142.7675102.6688182.86622.99e-12||334305.1818148.8057156.3761110.3439202.40822.77e-11||340310.0909150.4975159.5934112.1866207.00034.16e-11||342311.7273151.0358160.6915112.8294208.55364.69e-11||--------------------------------------------------------------------------||370332.0909158.5717173.5192119.5852227.45322.87e-10||397351.7273165.8385185.8887125.7134246.06411.41e-09||427373.5454173.9127199.6327132.2074267.0586.51e-09||445386.6364178.7573207.8791135.9845279.77361.45e-08||482413.5454188.7155224.83143.5408306.11915.93e-08||--------------------------------------------------------------------------||515437.5454197.5971239.9483150.1031329.79351.65e-07||545459.3636205.6714253.6923155.9623351.42223.62e-07||583487215.8987271.1013163.2743378.92838.32e-07||596494.8788219.3976275.4812164.6331386.32931.11e-06||620509.4243225.8569283.5673166.951400.18361.88e-06||--------------------------------------------------------------------------||670539.7273239.314300.4133171.1152429.71145.27e-06||675542.7576240.6597302.0979171.4897432.70615.80e-06||733577.9091254.969322.9401176.861469.0191 .0000147||841643.3636279.1917364.1719187.8796540.4643 .0000515||852650.0303281.6588368.3715188.9058547.8372 .0000575||--------------------------------------------------------------------------||915688.2121294.2187393.9934196.3119591.6749 .0000937||941703.9697299.4022404.5675199.2493609.8857 .0001125||979727306.978420.022203.4389636.6051 .0001441||995734.7576310.1678424.5898204.0643645.1152 .0001609||1032748.2121317.5443430.6678202.7468658.5889 .0002127||--------------------------------------------------------------------------||1141787.8485335.6531452.1953200.7097703.681 .0004248||1321853.303365.5577487.7454191.5434783.9473 .0012492||1386876.9394376.3565500.5829186.9499814.2158 .0017585||1400882.0303378.2173503.813186.4392821.1869 .0018625||1407884.5757379.1476505.4281186.1745824.6817 .0019162|+--------------------------------------------------------------------------+```:::::: {.content-visible when-format="pdf"}```{r eval=FALSE}+--------------------------------------------------------------------------+| _time _rmst1 _rmst0 _diff 95%CI lower 95%CI upper pvalue||--------------------------------------------------------------------------||111000 . ||221.989011 .010989-.0104304 .0324084 .3146368||332.945055 .0549451-.0009099 .1108 .0538507||554.791209 .2087912 .0549289 .3626535 .0078217||665.692307 .3076923 .0995576 .5158269 .0037617||--------------------------------------------------------------------------||887.45055 .5494505 .2224352 .8764658 .0009908||998.318682 .6813186 .29139151.071246 .0006156||505038.9024211.097587.53926114.65599.80e-10||515437.5454197.5971239.9483150.1031329.79351.65e-07||995734.7576310.1678424.5898204.0643645.1152 .0001609||1032748.2121317.5443430.6678202.7468658.5889 .0002127||--------------------------------------------------------------------------||1141787.8485335.6531452.1953200.7097703.681 .0004248||1321853.303365.5577487.7454191.5434783.9473 .0012492||1386876.9394376.3565500.5829186.9499814.2158 .0017585||1400882.0303378.2173503.813186.4392821.1869 .0018625||1407884.5757379.1476505.4281186.1745824.6817 .0019162|+--------------------------------------------------------------------------+```:::{width=70%}
