Les méthodes non paramétriques portent généralement sur l’analyse des fonctions de survie (\(S(t\))) moins sur les fonctions de répartitions (\(F(t)\))1, plus rarement sur les mesures d’incidence données par le risque cumulé. Deux méthodes d’estimations sont proposées : la méthode dite actuarielle et la méthode dite de Kaplan & Meier. Ces deux approches sont adaptées à des mesures différentes de la durée : plutôt discrète/groupée pour la technique actuarielle et plutôt continue pour Kaplan-Meier (KM). Cela induit un traitement différent de la censure dans l’estimation. La seconde est de très très loin la plus utilisée, médecine oblige, et en partie en raison des tests de comparaison, plus ou moins pertinents, qu’elle permet de réaliser.
Important
J’insiste sur la nécessité de passer par cette étape avant de se lancer corps perdu dans des modèles, comme ceux à durée discrète/groupée.
Egalement très utile, la comparaison graphique de courbes de séjour permet de repérer rapidement des violations fortes de l’hypothèse de proportionalité des risques, ou des situations de quasi immunité.
Concernant les tests non paramétriques, ceux utilsant la technique du logrank, présentent beaucoup de défauts. Malheureusement encore très peu diffusée dans les sciences sociales, la comparaison des RMST (Restricted Mean of Survival Time), dérivée de l’estimateur de Kaplan Meier, me semble une solution largement supérieure, tant au niveau statistique qu’au niveau interprétatif.
5.1 Les fonctions de survie/séjour
5.1.1 Les variables d’analyse
On a un échantillon aléatoire de \(n\) individus avec:
Des indicateurs de fin d’épisode \(e_1,e_2,....,e_k\) avec \(e_i=0\) si censure à droite et \(e_i=1\) si évènement observé pendant la période d’observation.
Des durées d’exposition au risque \(t_1,t_2,....,t_k\) jusqu’à l’évènement ou la censure.
En théorie, il ne peut pas y avoir d’évènement en \(t=0\).
5.1.2 Calcul de la fonction de survie
Rappel: La fonction de survie donne la probabilité que l’évènement survienne après \(t_i\), soit \(S(t_i)=P(T>t_i)\). Pour survivre en \(t_i\), il faut donc avoir survécu en \(t_{i-1}\), \(t_{i-2}\), …., \(t_{1}\).
La fonction de survie renvoie donc des probabilités conditionnelles: on survit en \(t_i\) conditionnellement au fait d’y avoir survécu avant. Il s’agit donc d’un produit de probabilités.
Soit \(d_i=\sum e_i\) le nombre d’évènements observés en \(t_i\), et \(r_i\) la population encore soumise au risque en \(i\). On peut mesurer l’intensité de l’évènement en \(t_i\) en calculant le quotient \(q(t_i)=\frac{d_i}{r_i}\).
Si le temps est strictement continu on devrait toujours avoir \(q(t_i)=\frac{1}{r_i}\).
\(S(t_i) = (1 - \frac{d_i}{r_i})\times{S(t_{i-1})} = S(t_i) = (1 - q(t_i))\times{S(t_{i-1})}\). En remplaçant \(S(t_{i-1})\) par sa valeur: \(S(t_i) = (1 - \frac{d_i}{r_i})\times(1 - \frac{d_{i-1}}{r_{i-1}})\times{S(t_{i-2})}\).
Au final, en remplaçant toutes les expressions de la survie jusqu’en \(t_0\) (\(S(0)=1\)):
On va analyser le risque de décéder (la survie) de personnes souffrant d’une insuffisance cardiaque. Le début de l’exposition est leur inscription dans un registre d’attente pour une greffe du coeur.
Les covariables sont dans un premier temps toutes fixes: l’année (year) et l’âge (age) à l’entrée dans le registre, et le fait d’avoir été opéré pour un pontage aorto-coronarien avant l’inscription (surgery).
Le début de l’exposition au risque est l’entrée dans le registre, la durée est mesurée en jour (stime). La variable évènement/censure est le décès (died). Les durées de la variable stime ont été regroupée par période de 30 jours pour réaliser des analyses à durée discrete. Cette nouvelle variable de durée a été appelé mois.
L’introduction d’une dimension dynamique, la greffe, est donnée par les informations contenues dans les variables transplant et wait.
La variable compet est une information simulée pour réaliser des analyses en risques concurrents.
Les bases en format .csv, .sas7bdat2 et .dta sont disponibles dans ce dépôt [lien]
Extrait de la base:
id
year
age
died
stime
surgery
transplant
wait
mois
compet
15
68
53
1
1
0
0
0
1
1
43
70
43
1
2
0
0
0
1
1
61
71
52
1
2
0
0
0
1
1
75
72
52
1
2
0
0
0
1
1
102
74
40
0
11
0
0
0
1
0
74
72
29
1
17
0
1
5
1
2
5.2 La méthode actuarielle
Estimation sur des intervalles définies par l’utilisateur.
Méthode dite «continue», estimation en milieu d’intevalle.
Méthode apropriée lorsque la durée est mesurée de manière discrète/groupée.
Méthode, hélas, quasiment abandonnée dans les sciences sociales où les durées sont rarement mesurées de manière exacte. L’absence de test de comparaison des fonctions de survie n’y est pas étranger, tout comme le lien de la méthode suivante (Kaplan-Meier) avec le modèle de Cox.
Contrairement à la méthode de Kaplan-Meier, la méthode actuarielle permet de calculer directement les quantiles de la durée.
5.2.1 Estimation
Echelle temporelle
La durée est divisée en \(J\) intervalles, en choisissant \(J\) points: \(t_0<t_1<...<t_J\) avec \(t_{J+1}=\infty\).
Calcul du Risk set
A \(t_{min}=0\), \(n_0=n\) individus soumis au risque: \(r_0=n_0\).
Le nombre d’exposé.e.s au risque sur un intervalle est calculé en soustrayant la moitié des cas censurés sur la longueur de l’intervalle: \(r_i=n_i- 0.5\times{c_i}\), avec \(n_i\) le nombre de personnes soumises au risque au début de l’intervalle et \(c_i\) le nombre d’observations censurées sur la longueur de l’intervalle. On suppose donc que les observations censurées \(c_i\) sont sorties de l’observation uniformément sur l’intervalle. Les cas censurés le sont en moyenne au millieu de l’intervalle.
Calcul de\(S(t_i)\)
On applique la méthode de la section précédente avec:
\[q(t_i)=\frac{d_i}{n_i - 0.5\times c_i}\]
Calcul de la durée médiane (ou autre quantiles)
Rappel: en raison de la présence de censures à droite, le dernier intervalle étant ouvert jusqu’à la dernière sortie d’observation, il n’est pas conseillé de calculer des durées moyennes. On préfère utiliser la médiane ou tout autre quantile lorsqu’ils sont calculables.
Définition: il s’agit de la durée telle que \(S(t_i)=0.5\).
Calcul: Comme on applique une méthode continue et monotone à l’intérieur d’intervalles, on ne peut pas calculer directement un point de coupure qui correspond à 50% de survivants. On doit donc trouver ce point par interpolation linéaire dans l’intervalle \([t_i;t_{i+1}[\) avec \(S(t_{i+1})\leq0.5\) et \(S(t_{i})>0.5\).
Les fonctions de survie avec la méthode dite actuarielle sont estimables avec le package discSurv. Avec le temps, il s’est étoffé, on peut maintenant paramatrer des intervalles (programmation pénible), mais les quantiles de la durée ne sont toujours pas estimables, ce qui est bien dommage, voire rend son utilisation peu intéressante.
Commande ltable, avec en option la paramétrisation des intervalles de durées. Voir la commande externe qlt (MT) qui calcule les durées médianes (+ autres quartiles) et qui recalcule la fonction de séjour avec une définition des intervalles de durées identique à celle de SAS .
A l’heure actuelle, aucune fonction à ma connaissance.
Sous une proc lifetest avec en option method=lifetable. On peut paramétrer les intervalles d’estimation avec l’option width.
5.2.2 Application
Les résultats qui suivent ont été estimés avec Stata en retenant la définition des bornes de Sas, plus pertinente à mon sens, avec des intervalles fixes de 30 jours.
Quantiles de la fonction de séjour type actuarielle - Bornes Sas
S(t)
t
0.90
13.977
0.75
37.623
0.50
104.729
0.25
906.993
0.10
.
Courbe de survie: estimation méthode actuarielle
Lecture des résultats: 102 jours après leur inscription dans le registre d’attente pour une greffe, 50% des malades sont toujours en vie. Au bout de 914 jours, 75% sont décédés.
5.3 La méthode de Kaplan-Meier
L’approche qui exploite toute l’information disponible est celle dite de Kaplan-Meier (KM).
Il y a autant d’intervalles que de durées où l’on observe au moins un évènement.
Au lieu d’utiliser des intervalles prédéterminés, l’estimateur KM va définir un intervalle entre chaque évènement enregistré.
La fonction de survie estimée par la méthode KM est une fonction en escalier (stairstep), d’où une estimation dite “discrète”.
Pour chaque intervalle, on compte le nombe d’évènements et le nombre de censures.
Méthode adaptée pour une mesure de la durée de type continue.
5.3.1 Estimation
Définition du Risk Set (\(r_i\))
S’il y a à la fois des évènements et des censures à une durée \(t_i\), les observations censurées sont considérées comme exposées au risque à ce moment, comme si elles étaient censurées très rapidement après. C’est la principale caractéristique de cette méthode, appelé également l’estimateur product-limit
\[r_i=r_{i-1}-d_{i-1}-c_{i-1}\]
Calcul de\(q_i\)
On applique la méthode de la section précédente avec:
\[q_i=\frac{d_i}{r_{i-1}-d_{i-1}-c_{i-1}}\]
Remarque: la variance de l’estimateur est obtenu par la méthode dite de Greenwood. Il n’y a pas d’intérêt particulier de la décrire dans ce support.
Récupération de la médiane
Il n’y a pas de méthode pour calculer directement la durée médiane (ou tout autre quantile) contrairement à l’approche actuarielle.
La définition retenue est donc conventionnelle. On va prendre la valeur de la durée qui se situe juste en dessous de 50% de survivant.e.s. Elle est donc définie tel que \(S(t)\leq0.5\). Attention, il n’est pas impossible que le % de survivant.e.s soit bien en deçà de 50% pour l’obtention cette durée médiane.
Les estimateurs sont obtenus avec fonction survfit du package survival. On peut obtenir des rendus graphiques de meilleures qualité avec le package survminer (fonction ggsurvplot)
Après avoir appelé les variables de durée et de censure en mode survival avec stset), le tableau des estimateurs est obtenu avec la commande sts list et le graphique avec sts graph.
Les resultats sont donnés dans la librairie lifeline par des fonctions au nom interminable. Je conseille plutôt l’utilisation de la librairie statmodels (se reporter à la section dédiée à Python).
L’estimation de Kaplan-Meier est affichée par défaut par la proc lifetest. Warning : le tableau affiché par SAS est particulièrement pénible à lire voire illisible, en particulier lorsque le nombre de censures est élevé, une ligne étant ajoutée pour chaque observation censurée. Je conseille de ne pas afficher cette partie de l’output (se reporter à la section SAS du chapitre programmation). On récupère pour le reste de l’output les valeurs de la durée pour S(t) =(.75,.5,.25) ainsi que le graphique, ce qui est suffisant.
5.3.2 Application
On reprend l’exemple précédent.
Afficher le tableau des estimateurs
Time Total Fail Lost Function Error [95% Conf. Int.]-------------------------------------------------------------------------------1103100.99030.00970.93310.99862102300.96120.01900.89980.9852399300.93200.02480.86270.9670596200.91260.02780.83880.9535694200.89320.03040.81550.9394892100.88350.03160.80400.9321991100.87380.03270.79260.92471190010.87380.03270.79260.92471289100.86400.03380.78110.91711688300.83450.03670.74740.89371785100.82470.03750.73630.88571884100.81490.03830.72530.87772183200.79520.03990.70340.86142881100.78540.04060.69260.85313080100.77560.04120.68190.84483179010.77560.04120.68190.84483278100.76570.04190.67100.83633577100.75570.04250.66030.82783676100.74580.04310.64950.81923775100.73580.04360.63880.81063974110.72590.04420.62820.80194072200.70570.04520.60680.78424370100.69560.04570.59610.77524569100.68560.04610.58550.76625068100.67550.04650.57500.75725167100.66540.04690.56450.74815366100.65530.04720.55410.73905865100.64520.04760.54370.72986164100.63520.04790.53330.72066663100.62510.04820.52300.71136862200.60490.04870.50260.69266960100.59480.04890.49240.68327259200.57470.04930.47220.66437757100.56460.04940.46210.65487856100.55450.04960.45210.64538055100.54440.04970.44220.63578154100.53430.04980.43230.62618553100.52430.04990.42240.61649052100.51420.04990.41250.60679651100.50410.04990.40270.596910050100.49400.04990.39300.587210249100.48390.04990.38330.577310948010.48390.04990.38330.577311047100.47360.04990.37330.567313146010.47360.04990.37330.567314945100.46310.04990.36320.557115344100.45260.04990.35310.546816543100.44210.04980.34300.536418042010.44210.04980.34300.536418641100.43130.04970.33270.525818840100.42050.04970.32250.515220739100.40970.04950.31230.504521938100.39890.04940.30220.493826337100.38810.04920.29210.483026536010.38810.04920.29210.483028535200.36600.04880.27140.460830833100.35490.04860.26120.449633432100.34380.04830.25100.438334031110.33270.04800.24090.427034229100.32120.04770.23050.415337028010.32120.04770.23050.415339727010.32120.04770.23050.415342726010.32120.04770.23050.415344525010.32120.04770.23050.415348224010.32120.04770.23050.415351523010.32120.04770.23050.415354522010.32120.04770.23050.415358321100.30590.04780.21560.400859620010.30590.04780.21560.400862019010.30590.04780.21560.400867018010.30590.04780.21560.400867517100.28790.04830.19760.384473316100.26990.04850.18020.367684115010.26990.04850.18020.367685214100.25070.04870.16160.349791513010.25070.04870.16160.349794112010.25070.04870.16160.349797911100.22790.04930.13940.329599510100.20510.04940.11830.3085[Résultats non reportés à partir de t=1000 ]-------------------------------------------------------------------------------
La durée durée médiane de survie est \(t=100\). Elle correspond à \(S(t)=0.4940\).
Quantiles de la fonction de séjour type Kaplan-Meier
S(t)
t
0.90
6
0.75
36
0.50
100
0.25
979
0.1
.
Courbe de survie: estimation méthode Kaplan-Meier
Courbe de survie: méthode Kaplan-Meier + CI
5.3.3 Quantités associées à l’estimateur Kaplan-Meier..
Le risque cumulé: estimateur de Nelson AAlen
Il est simplément égal à:
\[H(t)=\sum_{t_i\leq k}q(t_i)\]
Risque cumulé: estimateur Nelson-Aalen
Le risque ou taux de hasard instantané
Nécessite l’estimateur de risque cumulé de Nelson-Aalen. Le risque est obtenu en lissant les différences - toujours positive - entre \(H(t)\) par la méthode dite du kernel (cf estimation de la densité des distributions). Elle permet d’obtenir une fonction continue avec la durée (paramétrables sur les largeurs des fenêtres de lissage). D’autres méthodes de lissage sont maintenant possibles, et de plus en plus utilisées, en particulier celles utilisant des splines.
Risque instantané: estimateur du Kernel
Note
Il n’est pas inutile de noter qu’il n’y a pas de formule toute faite pour obtenir des valeurs du risque instantané. Ce type de méthode par lissage est pleinement paramétrable, par exemple sa fenêtre, ce qui implique que son profil varie d’un paramétrage à l’autre. Le graphique précédent a été fait avec Stata, si on utilisait le package muhaz on visualiserait une courbe différente… mais on pourrait retrouver celle qui est représenté ici en changeant les paramètres de lissage.
Courbe de survie: estimation méthode actuarielleCourbe de survie: estimation méthode Kaplan-MeierCourbe de survie: méthode Kaplan-Meier + CIRisque cumulé: estimateur Nelson-AalenRisque instantané: estimateur du Kernel
malheureusement, mais cela dépendra des options des logiciels↩︎
---#title: "**Estimations des fonctions de survie**"---# Estimations des fonctions de survieLes méthodes non paramétriques portent généralement sur l'analyse des fonctions de survie ($S(t$)) moins sur les fonctions de répartitions ($F(t)$)^[malheureusement, mais cela dépendra des options des logiciels], plus rarement sur les mesures d'incidence données par le risque cumulé.Deux méthodes d'estimations sont proposées : la méthode dite **actuarielle** et la méthode dite de **Kaplan & Meier**. Ces deux approches sont adaptées à des mesures différentes de la durée : plutôt discrète/groupée pour la techniqueactuarielle et plutôt continue pour Kaplan-Meier (KM). Cela induit un traitement différent de la censure dans l'estimation. La seconde est de très très loin la plus utilisée, médecine oblige, et en partie en raison des tests de comparaison, plus ou moins pertinents, qu'elle permet de réaliser. ::: callout-important- J'insiste sur la nécessité de passer par cette étape avant de se lancer *corps perdu* dans des modèles, comme ceux à durée discrète/groupée. - Egalement très utile, la comparaison graphique de courbes de séjour permet de repérer rapidement des violations fortes de l'hypothèse de proportionalité des risques, ou des situations de quasi *immunité*.- Concernant les tests non paramétriques, ceux utilsant la technique du *logrank*, présentent beaucoup de défauts. Malheureusement encore très peu diffusée dans les sciences sociales, la comparaison des RMST (*Restricted Mean of Survival Time*), dérivée de l'estimateur de Kaplan Meier, me semble une solution largement supérieure, tant au niveau statistique qu'au niveau interprétatif. :::## Les fonctions de survie/séjour### Les variables d'analyseOn a un échantillon aléatoire de $n$ individus avec:- Des indicateurs de fin d'épisode $e_1,e_2,....,e_k$ avec $e_i=0$ si censure à droite et $e_i=1$ si évènement observé pendant la période d'observation.- Des durées d'exposition au risque $t_1,t_2,....,t_k$ jusqu'à l'évènement ou la censure.- En théorie, il ne peut pas y avoir d'évènement en $t=0$. ### Calcul de la fonction de survieRappel: La fonction de survie donne la probabilité que l'évènementsurvienne après $t_i$, soit $S(t_i)=P(T>t_i)$.Pour survivre en $t_i$, il faut donc avoir survécu en $t_{i-1}$, $t_{i-2}$,...., $t_{1}$. La fonction de survie renvoie donc des probabilités conditionnelles:on survit en $t_i$ conditionnellement au fait d'y avoir survécu avant. Ils'agit donc d'un produit de probabilités. Soit $d_i=\sum e_i$ le nombre d'évènements observés en $t_i$, et $r_i$ lapopulation encore soumise au risque en $i$. On peut mesurer l'intensitéde l'évènement en $t_i$ en calculant le quotient $q(t_i)=\frac{d_i}{r_i}$. Si le temps est strictement continu on devrait toujours avoir $q(t_i)=\frac{1}{r_i}$.$S(t_i) = (1 - \frac{d_i}{r_i})\times{S(t_{i-1})} = S(t_i) = (1 - q(t_i))\times{S(t_{i-1})}$.En remplaçant $S(t_{i-1})$ par sa valeur:$S(t_i) = (1 - \frac{d_i}{r_i})\times(1 - \frac{d_{i-1}}{r_{i-1}})\times{S(t_{i-2})}$.Au final, en remplaçant toutes les expressions de la survie jusqu'en $t_0$($S(0)=1$): ::: {.box_img}$$S(t_i)=\displaystyle \prod_{t_i\leq{k}} (1-q(t_i))$$:::::: callout-note## Application pour la suite du support* On va analyser le risque de décéder (la survie) de personnes souffrant d'une insuffisance cardiaque. Le début de l'exposition est leur inscription dans un registre d'attente pour une greffe du coeur.* Les covariables sont dans un premier temps toutes fixes: l'année (*year*) et l'âge (*age*) à l'entrée dans le registre, et le fait d'avoir été opéré pour un pontage aorto-coronarien avant l'inscription (*surgery*). * Le début de l'exposition au risque est l'entrée dans le registre, la durée est mesurée en jour (*stime*). La variable évènement/censure est le décès (*died*). Les durées de la variable *stime* ont été regroupée par période de 30 jours pour réaliser des analyses à durée discrete. Cette nouvelle variable de durée a été appelé *mois*.* L'introduction d'une dimension dynamique, la greffe, est donnée par les informations contenues dans les variables *transplant* et *wait*.* La variable *compet* est une information simulée pour réaliser des analyses en risques concurrents. - Les bases en format .csv, .sas7bdat^[juste pour le souvenir] et .dta sont disponibles dans ce dépôt [[lien](https://github.com/mthevenin/analyse_duree/tree/main/bases)]Extrait de la base: | id | year | age | died | stime | surgery | transplant | wait | mois | compet ||-----|------|-----|------|-------|---------|------------|------|------|--------|| 15 | 68 | 53 | 1 | 1 | 0 | 0 | 0 | 1 | 1 || 43 | 70 | 43 | 1 | 2 | 0 | 0 | 0 | 1 | 1 || 61 | 71 | 52 | 1 | 2 | 0 | 0 | 0 | 1 | 1 || 75 | 72 | 52 | 1 | 2 | 0 | 0 | 0 | 1 | 1 || 102 | 74 | 40 | 0 | 11 | 0 | 0 | 0 | 1 | 0 || 74 | 72 | 29 | 1 | 17 | 0 | 1 | 5 | 1 | 2 |:::## La méthode actuarielle* Estimation sur des intervalles définies par l'utilisateur.* Méthode dite «continue», estimation en milieu d'intevalle.* Méthode apropriée lorsque la durée est mesurée de manière discrète/groupée.* Méthode, hélas, quasiment abandonnée dans les sciences sociales où les durées sont rarement mesurées de manière exacte. L'absence de test de comparaison des fonctions de survie n'y est pas étranger, tout comme le lien de la méthode suivante (Kaplan-Meier) avec le modèle de Cox.- Contrairement à la méthode de Kaplan-Meier, la méthode actuarielle permet de calculer directement les quantiles de la durée.### Estimation**Echelle temporelle**La durée est divisée en $J$ intervalles, en choisissant $J$ points:$t_0<t_1<...<t_J$ avec $t_{J+1}=\infty$.**Calcul du Risk set**- A $t_{min}=0$, $n_0=n$ individus soumis au risque: $r_0=n_0$.- Le nombre d'exposé.e.s au risque sur un intervalle est calculé en soustrayant la moitié des cas censurés sur la longueur de l'intervalle: $r_i=n_i- 0.5\times{c_i}$, avec $n_i$ le nombre de personnes soumises au risque au début de l'intervalle et $c_i$ le nombre d'observations censurées sur la longueur de l'intervalle. On suppose donc que les observations censurées $c_i$ sont sorties de l'observation uniformément sur l'intervalle. Les cas censurés le sont en moyenne au millieu de l'intervalle. <br>**Calcul de** $S(t_i)$\On applique la méthode de la section précédente avec:::: {.box_img}$$q(t_i)=\frac{d_i}{n_i - 0.5\times c_i}$$:::**Calcul de la durée médiane (ou autre quantiles)** *Rappel*: en raison de la présence de censures à droite, le dernierintervalle étant ouvert jusqu'à la dernière sortie d'observation, iln'est pas conseillé de calculer des durées moyennes. On préfère utiliserla médiane ou tout autre quantile lorsqu'ils sont calculables. **Définition**: il s'agit de la durée telle que $S(t_i)=0.5$. *Calcul*: Comme on applique une méthode continue et monotone àl'intérieur d'intervalles, on ne peut pas calculer directement un pointde coupure qui correspond à 50% de survivants. On doit donc trouver cepoint par interpolation linéaire dans l'intervalle $[t_i;t_{i+1}[$ avec$S(t_{i+1})\leq0.5$ et $S(t_{i})>0.5$.**R-Stata-Python-Sas** ::: panel-tabset#### RLes fonctions de survie avec la méthode dite actuarielle sont estimables avec le package **`discSurv`**. Avec le temps, il s'est étoffé, on peut maintenant paramatrer des intervalles (programmation pénible), mais les quantiles de la durée ne sont toujours pas estimables, ce qui est bien dommage, voire rend son utilisation peu intéressante. #### StataCommande `ltable`, avec en option la paramétrisation des intervalles dedurées. Voir la commande externe `qlt` (MT) qui calcule les duréesmédianes (+ autres quartiles) et qui recalcule la fonction de séjouravec une définition des intervalles de durées identique à celle de SAS {{< fa solid cross>}}.#### PythonA l'heure actuelle, aucune fonction à ma connaissance.#### Sas {{< fa solid cross>}}Sous une `proc lifetest` avec en option `method=lifetable`. On peutparamétrer les intervalles d'estimation avec l'option `width`.:::### ApplicationLes résultats qui suivent ont été estimés avec Stata en retenant la définition des bornes de Sas, plus pertinente à mon sens, avec des intervalles fixes de 30 jours.```{r eval=FALSE}#| code-fold: true#| code-summary: "**Afficher le tableau des estimateurs**" +----------------------------------------------+ | t0 t1 survival CI 95% low CI 95% up | |----------------------------------------------| 1. | 0 30 1 . . | 2. | 30 60 .7853659 .6925991 .8530615 | 3. | 60 90 .6461871 .5449008 .7304808 | 4. | 90 120 .525027 .4232338 .6170507 | 5. | 120 150 .4740535 .3737563 .5677139 | |----------------------------------------------| 6. | 150 180 .4636348 .3637283 .5575485 | 7. | 180 210 .4425605 .3435417 .5368989 | 8. | 210 240 .4105681 .3132064 .5052779 | 9. | 240 270 .3997637 .3030412 .4945301 | 10. | 270 300 .3888113 .2927645 .4836136 | |----------------------------------------------| 11. | 300 330 .3665935 .2720434 .4613676 | 12. | 330 360 .3554846 .2617823 .4501585 | 13. | 360 390 .3216289 .2308275 .4157428 | 14. | 390 420 .3216289 .2308275 .4157428 | 15. | 420 450 .3216289 .2308275 .4157428 | |----------------------------------------------| 16. | 480 510 .3216289 .2308275 .4157428 | 17. | 510 540 .3216289 .2308275 .4157428 | 18. | 540 570 .3216289 .2308275 .4157428 | 19. | 570 600 .3216289 .2308275 .4157428 | 20. | 600 630 .3059397 .2154747 .4009653 | |----------------------------------------------| 21. | 660 690 .3059397 .2154747 .4009653 | 22. | 720 750 .2884574 .1981834 .3848506 | 23. | 840 870 .2704288 .1806664 .3680736 | 24. | 900 930 .2517786 .1628919 .3505543 | 25. | 930 960 .2517786 .1628919 .3505543 | |----------------------------------------------| 26. | 960 990 .2517786 .1628919 .3505543 | 27. | 990 1020 .2288896 .1404089 .3303913 | 28. | 1020 1050 .2060007 .1191749 .3093143 | 29. | 1140 1170 .1831117 .0991601 .2873401 | 30. | 1320 1350 .1831117 .0991601 .2873401 | |----------------------------------------------| 31. | 1380 1410 .1831117 .0991601 .2873401 | 32. | 1560 1590 .1464894 .0645215 .2602391 | 33. | 1770 1800 .1464894 .0645215 .2602391 | 34. | 1800 . .1464894 .0645215 .2602391 | +----------------------------------------------+```|**S(t)** | **t** | |---------|--------|| 0.90 | 13.977 | | 0.75 | 37.623 | | 0.50 |104.729 | | 0.25 |906.993 | | 0.10 |. | : Quantiles de la fonction de séjour type actuarielle - Bornes Sas::: {.box_img}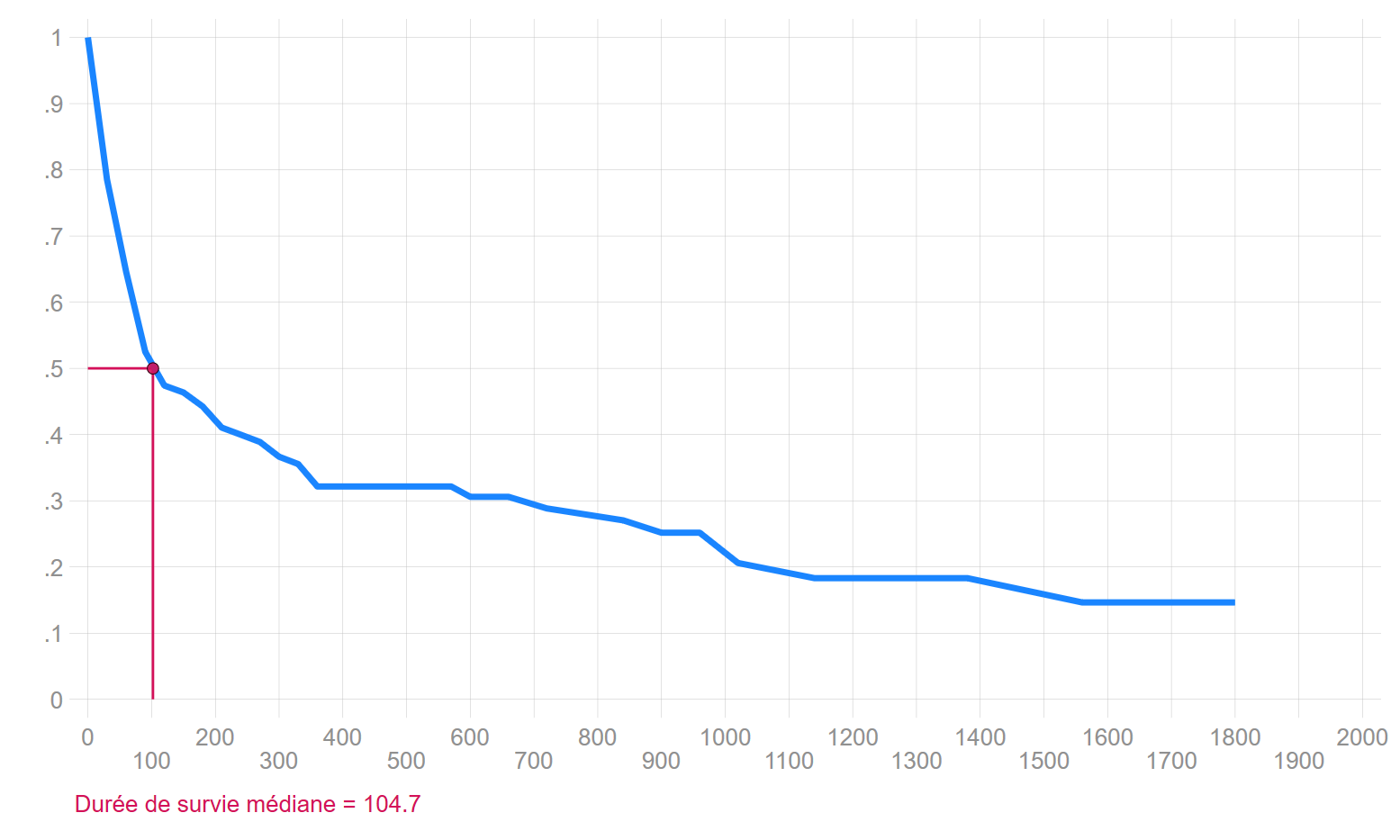{width="70%"}:::Lecture des résultats: 102 jours après leur inscription dans le registre d'attente pour unegreffe, 50% des malades sont toujours en vie. Au bout de 914 jours, 75% sont décédés.## La méthode de Kaplan-Meier- L'approche qui exploite toute l'information disponible est celle dite de **Kaplan-Meier** (*KM*).- Il y a autant d'intervalles que de durées où l'on observe au moins un évènement.- Au lieu d'utiliser des intervalles prédéterminés, l'estimateur KM va définir un intervalle entre chaque évènement enregistré.- La fonction de survie estimée par la méthode KM est une fonction en escalier (stairstep), d'où une estimation dite "discrète".- Pour chaque intervalle, on compte le nombe d'évènements et le nombre de censures.- Méthode adaptée pour une mesure de la durée de type continue.### Estimation**Définition du Risk Set (**$r_i$)S'il y a à la fois des évènements et des censures à une durée $t_i$, lesobservations censurées sont considérées comme exposées au risque à cemoment, comme si elles étaient censurées très rapidement après. C'est laprincipale caractéristique de cette méthode, appelé égalementl'estimateur ***product-limit***$$r_i=r_{i-1}-d_{i-1}-c_{i-1}$$\<br>**Calcul de** $q_i$\<br> On applique la méthode de la section précédente avec:::: {.box_img}$$q_i=\frac{d_i}{r_{i-1}-d_{i-1}-c_{i-1}}$$:::*Remarque*: la variance de l'estimateur est obtenu par la méthode dite de *Greenwood*. Il n'y a pas d'intérêt particulier de la décrire dans ce support. **Récupération de la médiane** Il n'y a pas de méthode pour calculer directement la durée médiane (outout autre quantile) contrairement à l'approche actuarielle. La définition retenue est donc conventionnelle. On va prendre la valeur de la durée qui se situe juste **en dessous** de50% de survivant.e.s. Elle est donc définie tel que $S(t)\leq0.5$. Attention, il n'est pas impossible que le % de survivant.e.s soit bienen deçà de 50% pour l'obtention cette durée médiane. **R-Stata-Python-Sas**::: panel-tabset#### RLes estimateurs sont obtenus avec fonction **`survfit`** du package `survival`. On peut obtenir des rendus graphiques de meilleures qualité avec le package `survminer` (fonction `ggsurvplot`)#### StataAprès avoir appelé les variables de durée et de censure en mode**survival** avec **`stset`**), le tableau des estimateurs est obtenu avec lacommande **`sts list`** et le graphique avec **`sts graph`**.#### PythonLes resultats sont donnés dans la librairie `lifeline` par des fonctionsau nom interminable. Je conseille plutôt l'utilisation de lalibrairie **`statmodels`** (se reporter à la section dédiée à Python).#### SAS {{<fa solid cross>}}L'estimation de Kaplan-Meier est affichée par défaut par la`proc lifetest`. ***Warning*** : le tableau affiché par SAS est particulièrement pénibleà lire voire illisible, en particulier lorsque le nombre de censures estélevé, une ligne étant ajoutée pour chaque observation censurée. Jeconseille de ne pas afficher cette partie de l'output (se reporter à lasection SAS du chapitre programmation). On récupère pour le reste del'output les valeurs de la durée pour S(t) =(.75,.5,.25) ainsi que legraphique, ce qui est suffisant.:::### ApplicationOn reprend l'exemple précédent.```{r eval=FALSE}#| code-fold: true#| code-summary: "**Afficher le tableau des estimateurs**"Time Total Fail Lost Function Error [95% Conf. Int.]------------------------------------------------------------------------------- 1 103 1 0 0.9903 0.0097 0.9331 0.9986 2 102 3 0 0.9612 0.0190 0.8998 0.9852 3 99 3 0 0.9320 0.0248 0.8627 0.9670 5 96 2 0 0.9126 0.0278 0.8388 0.9535 6 94 2 0 0.8932 0.0304 0.8155 0.9394 8 92 1 0 0.8835 0.0316 0.8040 0.9321 9 91 1 0 0.8738 0.0327 0.7926 0.9247 11 90 0 1 0.8738 0.0327 0.7926 0.9247 12 89 1 0 0.8640 0.0338 0.7811 0.9171 16 88 3 0 0.8345 0.0367 0.7474 0.8937 17 85 1 0 0.8247 0.0375 0.7363 0.8857 18 84 1 0 0.8149 0.0383 0.7253 0.8777 21 83 2 0 0.7952 0.0399 0.7034 0.8614 28 81 1 0 0.7854 0.0406 0.6926 0.8531 30 80 1 0 0.7756 0.0412 0.6819 0.8448 31 79 0 1 0.7756 0.0412 0.6819 0.8448 32 78 1 0 0.7657 0.0419 0.6710 0.8363 35 77 1 0 0.7557 0.0425 0.6603 0.8278 36 76 1 0 0.7458 0.0431 0.6495 0.8192 37 75 1 0 0.7358 0.0436 0.6388 0.8106 39 74 1 1 0.7259 0.0442 0.6282 0.8019 40 72 2 0 0.7057 0.0452 0.6068 0.7842 43 70 1 0 0.6956 0.0457 0.5961 0.7752 45 69 1 0 0.6856 0.0461 0.5855 0.7662 50 68 1 0 0.6755 0.0465 0.5750 0.7572 51 67 1 0 0.6654 0.0469 0.5645 0.7481 53 66 1 0 0.6553 0.0472 0.5541 0.7390 58 65 1 0 0.6452 0.0476 0.5437 0.7298 61 64 1 0 0.6352 0.0479 0.5333 0.7206 66 63 1 0 0.6251 0.0482 0.5230 0.7113 68 62 2 0 0.6049 0.0487 0.5026 0.6926 69 60 1 0 0.5948 0.0489 0.4924 0.6832 72 59 2 0 0.5747 0.0493 0.4722 0.6643 77 57 1 0 0.5646 0.0494 0.4621 0.6548 78 56 1 0 0.5545 0.0496 0.4521 0.6453 80 55 1 0 0.5444 0.0497 0.4422 0.6357 81 54 1 0 0.5343 0.0498 0.4323 0.6261 85 53 1 0 0.5243 0.0499 0.4224 0.6164 90 52 1 0 0.5142 0.0499 0.4125 0.6067 96 51 1 0 0.5041 0.0499 0.4027 0.5969 100 50 1 0 0.4940 0.0499 0.3930 0.5872 102 49 1 0 0.4839 0.0499 0.3833 0.5773 109 48 0 1 0.4839 0.0499 0.3833 0.5773 110 47 1 0 0.4736 0.0499 0.3733 0.5673 131 46 0 1 0.4736 0.0499 0.3733 0.5673 149 45 1 0 0.4631 0.0499 0.3632 0.5571 153 44 1 0 0.4526 0.0499 0.3531 0.5468 165 43 1 0 0.4421 0.0498 0.3430 0.5364 180 42 0 1 0.4421 0.0498 0.3430 0.5364 186 41 1 0 0.4313 0.0497 0.3327 0.5258 188 40 1 0 0.4205 0.0497 0.3225 0.5152 207 39 1 0 0.4097 0.0495 0.3123 0.5045 219 38 1 0 0.3989 0.0494 0.3022 0.4938 263 37 1 0 0.3881 0.0492 0.2921 0.4830 265 36 0 1 0.3881 0.0492 0.2921 0.4830 285 35 2 0 0.3660 0.0488 0.2714 0.4608 308 33 1 0 0.3549 0.0486 0.2612 0.4496 334 32 1 0 0.3438 0.0483 0.2510 0.4383 340 31 1 1 0.3327 0.0480 0.2409 0.4270 342 29 1 0 0.3212 0.0477 0.2305 0.4153 370 28 0 1 0.3212 0.0477 0.2305 0.4153 397 27 0 1 0.3212 0.0477 0.2305 0.4153 427 26 0 1 0.3212 0.0477 0.2305 0.4153 445 25 0 1 0.3212 0.0477 0.2305 0.4153 482 24 0 1 0.3212 0.0477 0.2305 0.4153 515 23 0 1 0.3212 0.0477 0.2305 0.4153 545 22 0 1 0.3212 0.0477 0.2305 0.4153 583 21 1 0 0.3059 0.0478 0.2156 0.4008 596 20 0 1 0.3059 0.0478 0.2156 0.4008 620 19 0 1 0.3059 0.0478 0.2156 0.4008 670 18 0 1 0.3059 0.0478 0.2156 0.4008 675 17 1 0 0.2879 0.0483 0.1976 0.3844 733 16 1 0 0.2699 0.0485 0.1802 0.3676 841 15 0 1 0.2699 0.0485 0.1802 0.3676 852 14 1 0 0.2507 0.0487 0.1616 0.3497 915 13 0 1 0.2507 0.0487 0.1616 0.3497 941 12 0 1 0.2507 0.0487 0.1616 0.3497 979 11 1 0 0.2279 0.0493 0.1394 0.3295 995 10 1 0 0.2051 0.0494 0.1183 0.3085[Résultats non reportés à partir de t=1000 ]-------------------------------------------------------------------------------```La durée durée médiane de survie est $t=100$. Elle correspond à $S(t)=0.4940$.| **S(t)** | **t** ||----------|-------|| 0.90 | 6 || 0.75 | 36 || 0.50 | 100 || 0.25 | 979 || 0.1 | . |: Quantiles de la fonction de séjour type Kaplan-Meier::: {.content-visible when-format="html"} ::: {layout-ncol=2} ::: {.box_img}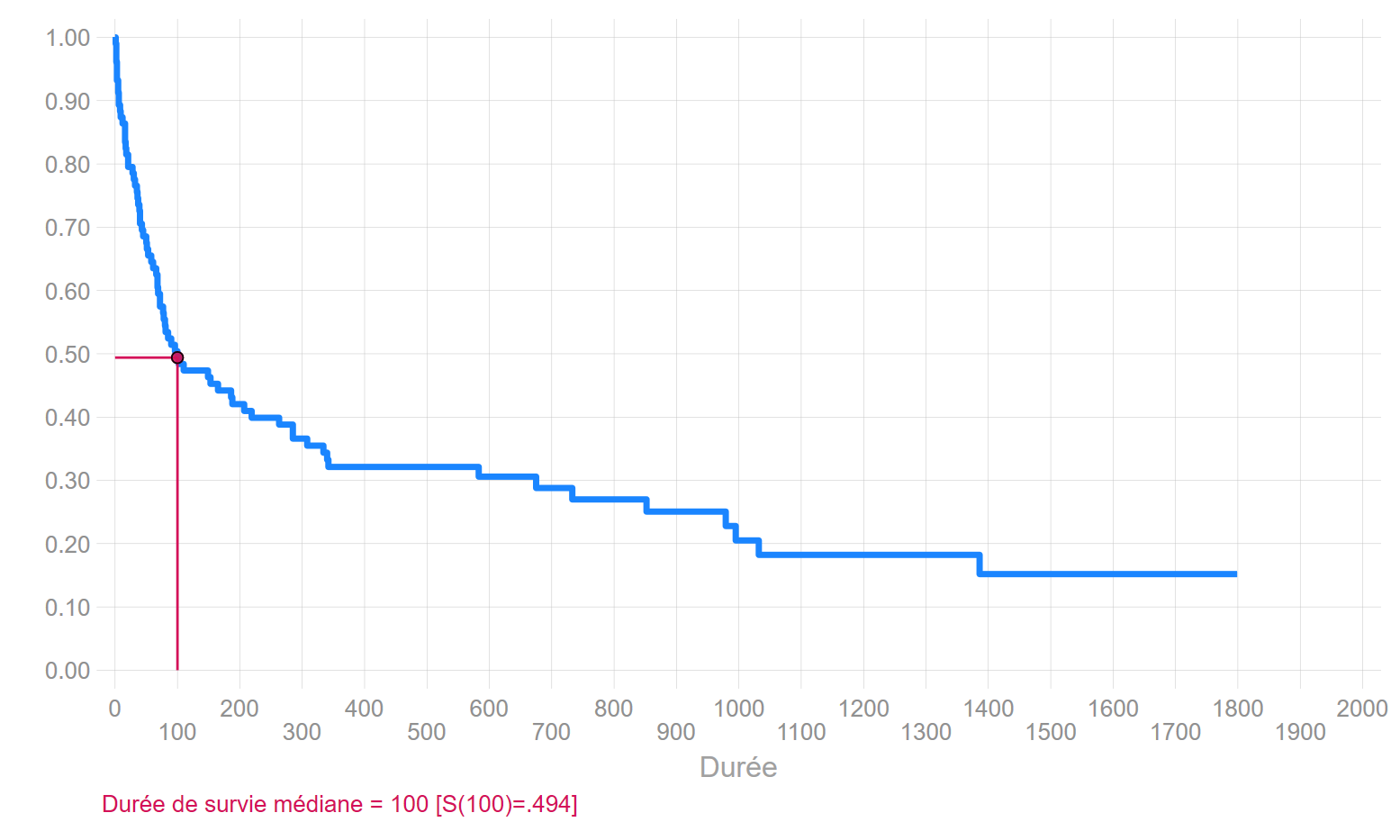{width="70%"}:::::: {.box_img}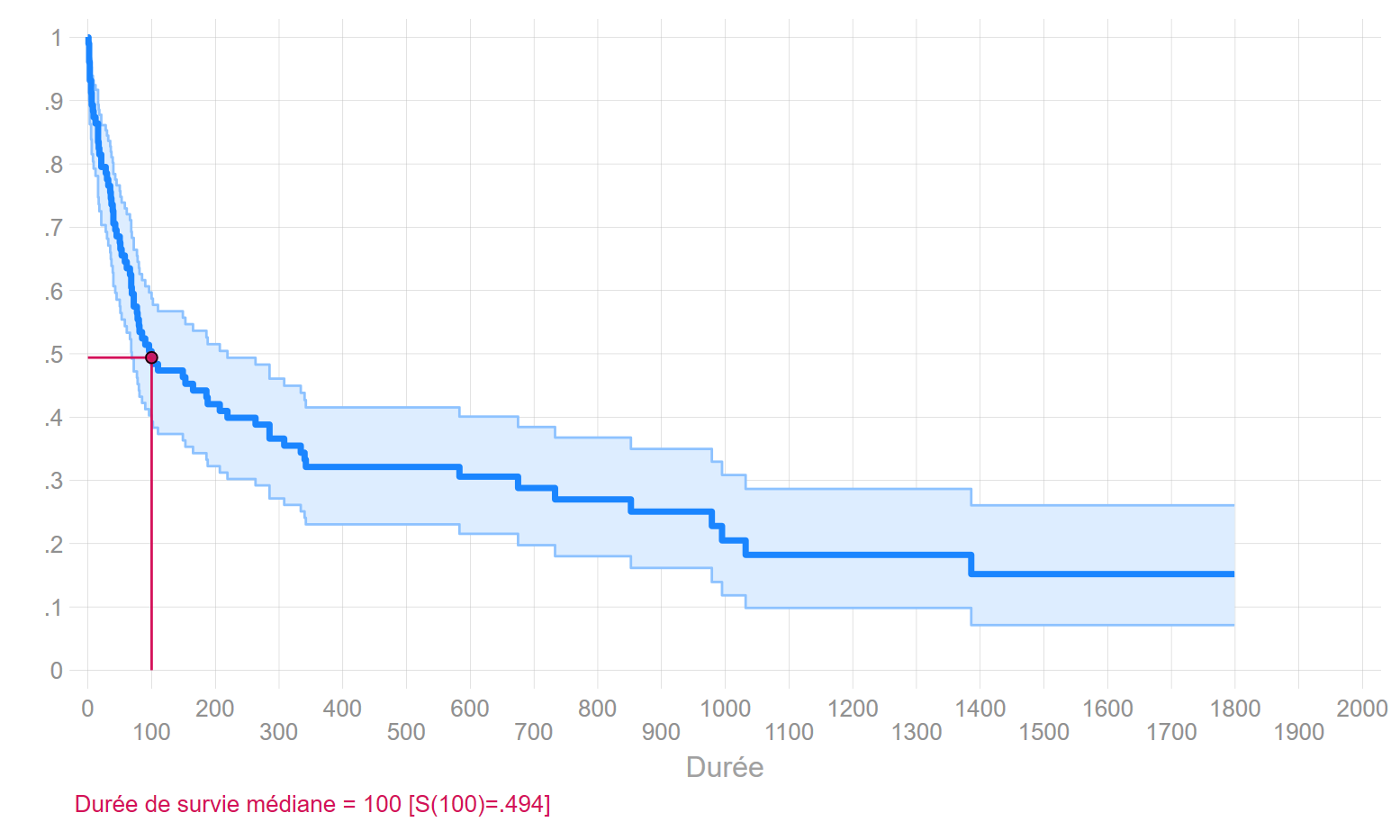{width="70%"}:::::::::::: {.content-visible when-format="pdf"}::: {.box_img}{width="70%"}:::::: {.box_img}{width="70%"}::::::### Quantités associées à l'estimateur Kaplan-Meier..**Le risque cumulé**: estimateur de Nelson AAlenIl est simplément égal à: $$H(t)=\sum_{t_i\leq k}q(t_i)$$::: {.box_img}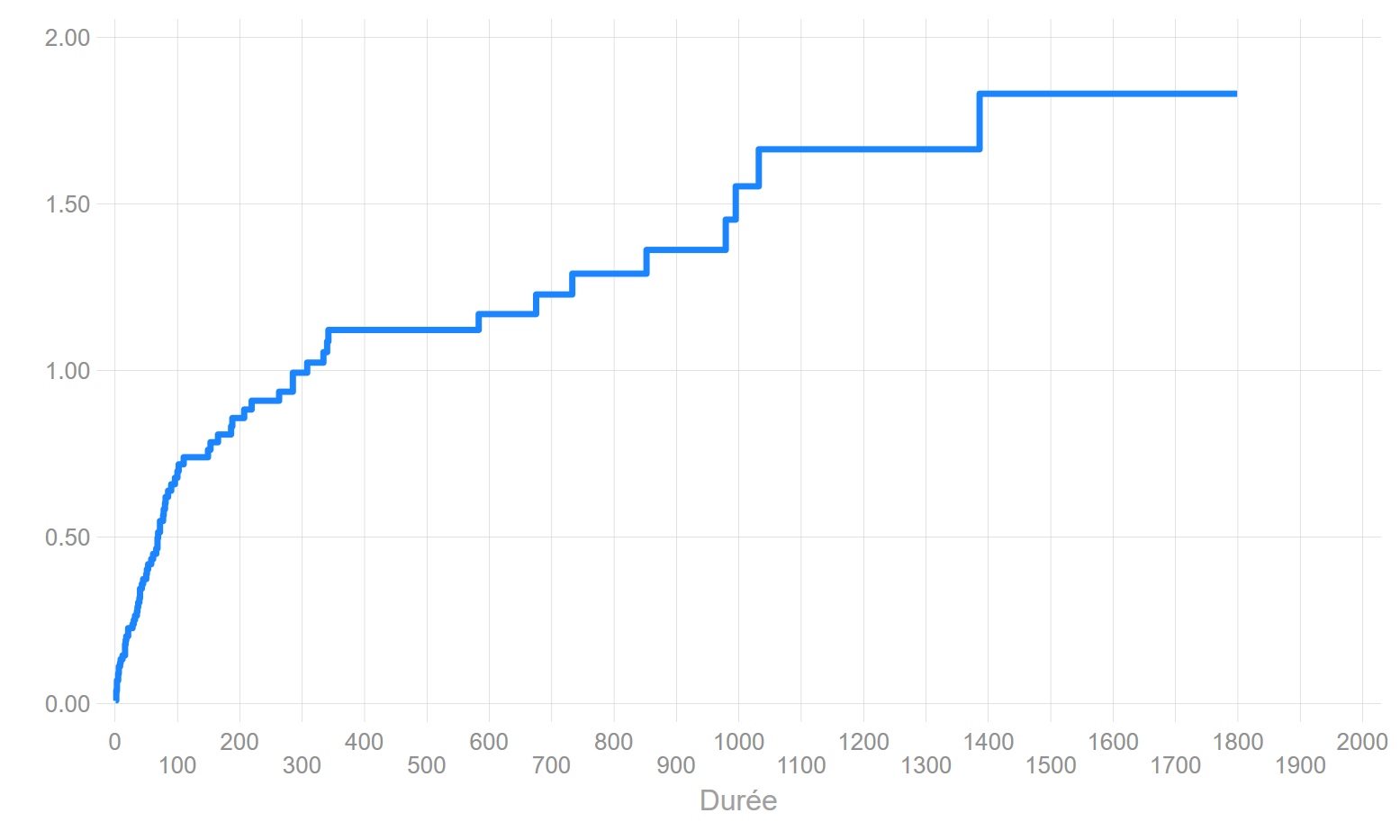{width="70%"}:::**Le risque ou taux de hasard instantané** Nécessite l'estimateur de risque cumulé de Nelson-Aalen. Le risque est obtenu en lissant les différences - toujours positive - entre $H(t)$ par la méthode ditedu **kernel** (cf estimation de la densité des distributions). Elle permet d'obtenirune fonction continue avec la durée(paramétrables sur les largeurs des fenêtres de lissage). D'autres méthodes de lissagesont maintenant possibles, et de plus en plus utilisées, en particulier celles utilisant des **splines**. ::: {.box_img}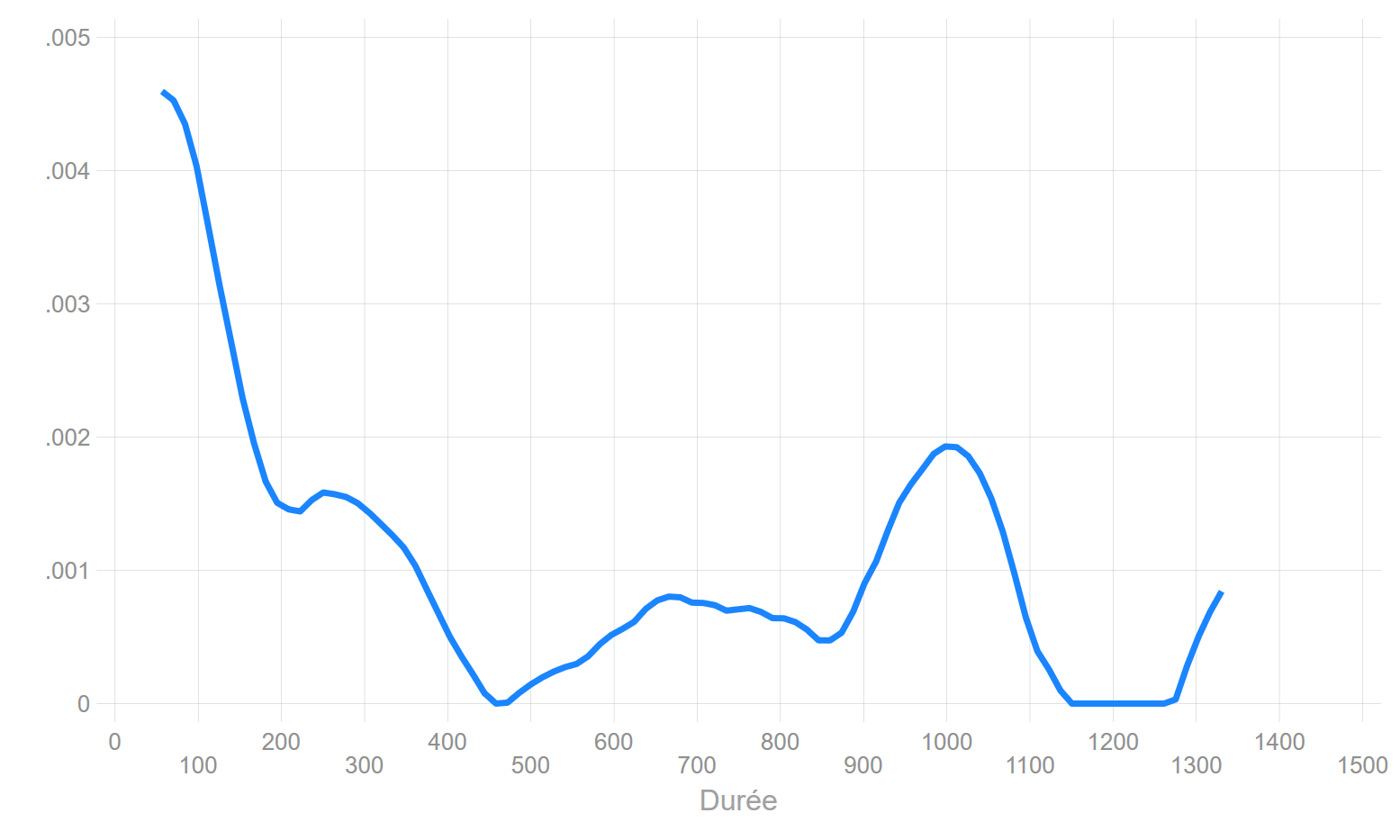{width="70%"}:::::: callout-noteIl n'est pas inutile de noter qu'il n'y a pas de *formule* toute faite pour obtenir des valeurs du risque instantané. Ce type de méthode par lissage est pleinement paramétrable, par exemple sa fenêtre, ce qui implique que son profil varie d'un paramétrage à l'autre. Le graphique précédent a été fait avec Stata, si on utilisait le package `muhaz` on visualiserait une courbe différente... mais on pourrait retrouver celle qui est représenté ici en changeant les paramètres de lissage.:::