9 Modèle à durée discrète
On va principalement traiter du modèle logistique à durée discrète.
- Par définition ce n’est pas un modèle à risques proportionnels, mais à Odds proportionnels. Toutefois en situation de rareté (p<0.1), l’Odds converge vers une probabilité, qui est une mesure du risque. Et donc les Odds ratio peuvent aisément se lire comme des rapports de probabilités.
- Le modèle à durée discrète est de type pleinement paramétrique, il est moins contraignant que le modèle de Cox si l’hypothèse de proportionnalité n’est pas respectée, car le modèle est directement ajusté par une fonction de la durée.
- Pour être estimé, la base de données doit être préalablement transformée en format long: sur les durées d’observation directement disponibles ou sur des regroupements de celles ci éventuellement de longueur différentes, ou sur les intervalles définis à partir des moments d’évènement lorsqu’il y a un nombre important d’évènements simultanés. (Kaplan-Meier et Cox).
- Ce modèle permet d’introduire bien plus simplement qu’avec le modèle de Cox un ensemble de covariables non fixes.
Avec un lien logistique, le modèle à durée discrète, avec seulement des covariables fixes, peut s’écrire:
\[log\left[\frac{P(Y=1\ |\ t_p,X_k)}{1-P(Y=1\ |\ t_p,X_k)}\right]= a_0 + \sum_{p}a_pf(t_p)+\sum_{k}b_kX_k\]
On restera ici sur la fonctions de lien logistique, mais bien évidemment les autres fonctions associées à la fonction de masse binomiale sont utilisables.
Le lien probit, est a ma connaissance très peut utilisé en analyse des durées. C’est bien évidemment lié aux lectures des paramètres estimés. On peut utiliser des formes standardisés sur l’échelle des probabilités avec des effets marginaux, mais ceux-ci ne pourront pas être généralisés sur l’ajustement de la durée se fait avec une forme quadratique ou à la présence d’une intéraction de quelque forme que ce soit (même problème si lien logistique).
Le lien complémentaire log-log, est une alternative bien plus intéressante en raison de son lien avec la relation entre fonction de séjour et risque cumulé. Son utilisation doit être néanmoins d’être réservée à des situations de rareté des probabilités conditionnelles (disons <.10, 0.5 préconisé), ce qui est souvent le cas en analyse de survie 1. Sous cette condition, on peut interpréter directement les estimateurs commes des rapports de risque au sens de l’analyse de survie. On pourra se reporter à l’explication de G.Rodrigez dont le support est en lien la bibliographie du document. Je ferai peut-être un jour une section dédiée dans la partie annexe. La construction mathématique est plutôt simple.
Pour information seulement car non testé. Développés dans le domaine l’épidémiologie, il existe des algorithmes forçant l’application du lien \(log(p)\) à une vraisemblance de type binomiale. On parle de modèle log-binomial. Il s’agit bien de la fonction de lien canonique associée à la vraisemblance d’un processus poissonien2 et dont les estimateurs sont indrectement interprétables en rapport de risques. Cette technique ne doit être envisagé qu’avec des incidences supérieurs à 20%. Je n’ai pas d’expérience particulière sur ce type de modèles 3, je ne suis donc pas capable de les évaluer en analyse de durée avec des durées très groupées, mais au niveau outils il semble que les solutions disponibles dans des packages R comme
logbinsoient à privilégier.
9.1 Organisation des données
Format long
Les données doivent être en format long: pour chaque individu, on a une ligne par durée observée ou par intevalle de durées jusqu’à l’évènement ou la censure. On retrouve le split des données du modèle de Cox pour introduire une variable dynamique, mais généralisé à des intervalles où aucun évènement n’est observé. Avec des données de type discrètes ou groupées, phénomène classique en sciences sociales, il y a souvent peu de différence entre un allongement aux temps d’évènement et aux temps d’observation.
Durée
La durée est dans un premier temps construite sous forme d’un simple compteur, par exemple \(t=1,2,3,4,5...\) (des valeurs non entières sont possibles). Le choix de la forme fonctionnelle de la durée sera présentée plus tard.
Variable évènement/censure
Si l’individu a connu l’évènement, elle prend la valeur 0 avant celui-ci. Au moment de l’évènement sa valeur est égale à 1. Pour les observations censurées, la variable prend toujours la valeur 0. seule la dernière ligne observées peut prendre une valeur non nulle4.
Application
On reprend les données de la base transplantation, mais les durées ont été regroupées par période de 30 jours. Il n’y a pas de durée mesurée comme nulle, et on a considéré que les 30 premiers jours représentaient, le premier mois d’exposition. Cette variable de durée se nomme mois.
Format d’origine
| id | year | age | surgery | mois | died |
|---|---|---|---|---|---|
| 1 | 67 | 30 | 0 | 2 | 1 |
La personne décède lors du deuxième intervalle de 30 jours
Format long et variables pour l’analyse
| id | year | age | surgery | mois | died | t |
|---|---|---|---|---|---|---|
| 1 | 67 | 30 | 0 | 2 | 0 | 1 |
| 1 | 67 | 30 | 0 | 2 | 1 | 2 |
9.2 Ajustement de la durée
Un des principaux enjeux réside dans la paramétrisation de la durée:
- Elle peut-être modélisée sous forme de fonction d’une variable de type quantitative/continue.
- Elle peut-être modélisée comme variable discrète, de type indicatrice \({0;1}\), sur tous les points d’observation ou sous forme de regroupements. Il doit y avoir au moins un évènement observé dans chaque intervalle.
Cox est également à l’origine du modèle à durée discrète (1973). Par rapport aux pratiques courantes, la différence repose sur les bornes intervalles, identiques à celles définies pour l’estimation de la courbe de survie KM ou du modèle semi-paramétrique, à savoir une définition sur les moments d’évènement. Avec un ajustement de la durée reposant sur des indicatrices (ajustement sur des variables discrètes), ce modèle est quasiment identique au modèle semi paramétrique.
On peut remarquer qu’en sciences sociales, avec des durées assez fortement groupées, les intervalles directement observés et les intervalles définis aux moments d’évènements sont souvent identiques et s’ils ne le sont pas c’est souvent en tout début ou en toute fin de la période d’observation/exposition. En cas d’ajustement de la durée par des indicatrices, la définition des bornes des intervalles aux moments des évènements permet de s’assurer de la présence d’au moins une occurence .
9.2.1 Ajustement avec une fonction quantitative de la durée
Le modèle étant paramétrique, on doit trouver une fonction qui ajuste le mieux les données. Toute transformation de la variable est possible: \(f(t)=a\times t\), \(f(t)=a\times log(t)\)……formes quadratiques. Les ajustements sous forme de splines cubiques tendent à se développer ces dernières années.
Pour sélectionner cette fonction, on peut tester différents modèles sans covariable additionnelle [\(g(y(t))=f(t)\)], et sélectionner la forme dont le critère d’information de type vraisemblance pénalisée (AIC, BIC) est le plus faible, avec au moins des différences de -6 ou -8.
Exemple:
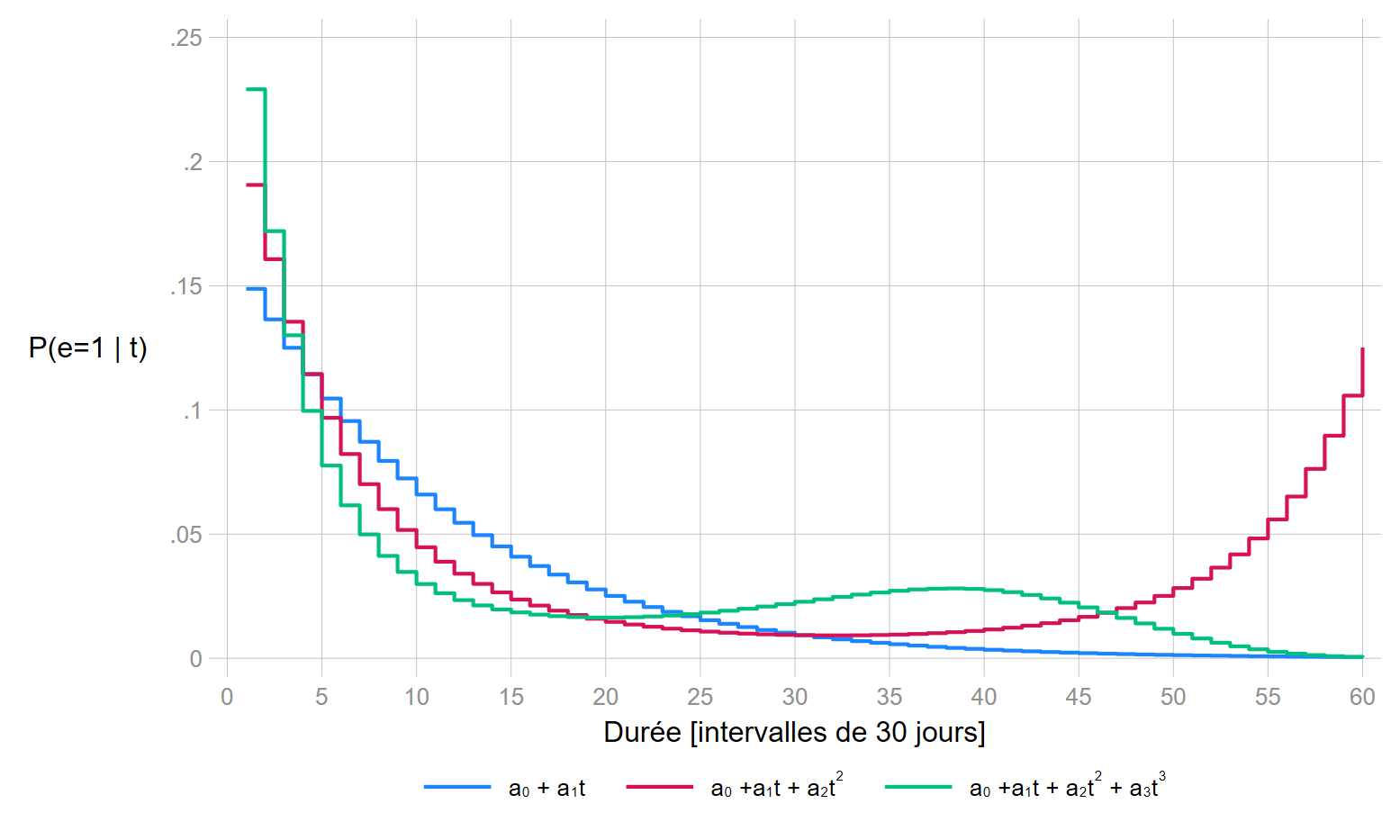
On va tester les paramétrisations suivantes: une forme linéraire stricte \(f(t)=a\times t\) et des effets quadratiques d’ordres 2 et 3: \(f(t)=a_1\times t + a_2\times t^{2}\) et \(f(t)=a_1\times t + a_2\times t^{2} + a_3\times t^{3}\).
Critères AIC
| \(f(t)\) | AIC |
|---|---|
| \(a\times t\) | 504 |
| \(a_1\times t + a_2\times t^{2}\) | 492 |
| \(a_1\times t + a_2\times t^{2} + a_3\times t^{3}\) | 486 |
On peut utiliser la troisième forme à savoir \(a_1\times t + a_2\times t^{2} + a_3\times t^{3}\) 5.
Estimation du modèle avec toutes les covariables
| Variables | OR - RR | Std. err | z | P>|z| | 95% IC |
|---|---|---|---|---|---|
| \(t\) | 0.678 | 0.057 | -4.52 | 0.000 | 0.587 ; 0.810 |
| \(t^2\) | 1.014 | 0.005 | +2.83 | 0.005 | 1.004 ; 1.024 |
| \(t^3\) | 1.000 | 0.000 | -2.11 | 0.035 | 1.000 ; 1.000 |
| \(year\) | 0.876 | 0.015 | -1.80 | 0.072 | 0.758 ; 1.012 |
| \(age\) | 1.034 | 0.163 | +2.27 | 0.023 | 1.005 ; 1.064 |
| \(surgery\) | 0.364 | 0.110 | -2.25 | 0.024 | 0.151 ; 0.877 |
| Constante | 0.440 | 0.110 | -3.29 | 0.001 | 0.270 ; 0.718 |
Remarque: les variables year et age ont été centrées sur leur moyenne pour rendre la constante interprétable. La constante reporte donc l’Odds de décéder lors des 30 premiers jours d’une personne dont l’âge et l’année à l’entrée dans le registre à l’âge moyen et à l’année moyenne, et qui n’a pas été opéré préalablement pour un pontage.
Si maintenant on estime un modèle de Cox sur ces données journalières groupées, on remarque que les résultats obtenus, et ce n’est pas une surprise, sont très proches.
| Variables | OR - RR | Std. err | z | P>|z| | 95% IC |
|---|---|---|---|---|---|
| \(year\) | 0.878 | 0.059 | -1.93 | 0.053 | 0.769 ; 1.002 |
| \(age\) | 1.029 | 0.014 | +2.13 | 0.033 | 1.002 ; 1.057 |
| \(surgery\) | 0.379 | 0.165 | -2.22 | 0.026 | 0.111 ; 0.892 |
9.2.2 Ajustement discret
- Il s’agit d’introduire la variable de durée dans le modèle comme une variable catégorielle (indicatrices).
- Cette option n’est pas conseillée si on a beaucoup de points d’observation, ce qui est le cas ici.
- A l’inverse, si peu de points d’observation la paramétrisation avec une durée continue n’est pas conseillé.
- La correction de la non proportionnalité peut être plus compliquée à mettre en oeuvre.
On va supposer que l’on ne dispose que de 4 intervalles d’observation. Pour l’exemple, on va créer ces points à partir des quartiles de la durée, et conserver pour chaque personne une seule observation par intervalle.
- \(t=1\): Entre le début de l’exposition et 4 mois.
- \(t=2\): Entre 5 mois et 11 mois .
- \(t=3\): Entre 12 mois et 23 mois.
- \(t=4\): 24 mois et plus.
On va estimer le risque globalement sur l’intervalle. La base sera plus courte que la précédente (197 observations pour 103 individus). Il ne sera plus possible ici d’interpréter les résultats en termes de rapport de probabilité, l’évènement devenant trop fréquent à l’intérieur de chaque intervalle.
| Variables | OR | Std. err | z | P>|z| | 95% IC |
|---|---|---|---|---|---|
| \(0-4 mois\) | 2.811 | 1.177 | +2.47 | 0.014 | 1.237 ; 6.387 |
| \(5-11 mois\) | ref | - | - | - | - |
| \(12-23 mois\) | 0.559 | 0.346 | -0.94 | 0.347 | 0.166 ; 1.881 |
| \(24-46 mois\) | 1.741 | 1.159 | +0.83 | 0.405 | 0.472 ; 6.417 |
| \(year\) | 0.816 | 0.076 | -2.18 | 0.029 | 0.680 ; 0.980 |
| \(age\) | 1.048 | 0.019 | +2.53 | 0.011 | 1.011 ; 1.087 |
| \(surgery\) | 0.330 | 0.166 | -2.21 | 0.027 | 0.123 ; 0.882 |
| Constante | 0.407 | 0.151 | 2.43 | 0.015 | 0.198 ; 0.840 |
On trouve des résultats proches de ceux éstimés avec un ajustement continu de la durée. C’est normal, la dirée fait office de variable d’ajustement peu ou pas corrélée avec les autres variables introduites.
| Variables | Ajustement discret | Ajustement continu |
|---|---|---|
| \(year\) | 0.816 | 0.876 |
| \(age\) | 1.048 | 1.034 |
| \(surgery\) | 0.330 | 0.364 |
Si la durée discrète/groupée sous tend une durée continue (ce qui est clairement le cas ici):
- L’ajustement avec des durées sous forme d’indicatrices correspond au modèle à durée discrète défini par Cox. Il est également assimilable à un modèle appelé exponential piecewice constant (soit un modèle de poisson).
- Si l’ajustement se fait en utilisation une transformation de la durée par une fonction:
- \(f(t)= log(t)\) correspond à un modèle de Weibull à risque proportionnel 6.
- Si l’ajustement se fait avec des splines cubiques, le modèle à durée discrète correspond à un modèle de type Parmar-Royston.
9.3 Proportionnalité des risques
Formellement un modèle logistique à durée discrète/groupée repose sur une hypothèse d’Odds proportionnels [Odds ratios constants pendant la durée d’observation]. Contrairement au modèle de Cox, l’estimation des probabilités (risque) n’est pas biaisée si l’hypothèse PH n’est pas respectée, les paramètres estimés seront considérés au pire comme des approximation…. problématique d’intéraction oblige.
Comme pour le modèle de Cox, la correction de la non proportionnalité peut se faire en intégrant une interaction avec la durée dans le modèle.
Avec un ajustement continue, on remarque de nouveau que le résultat du modèle est très proche de celui estimé avec un modèle de Cox.
| Variables | OR - RR | Std. err | z | P>|z| | 95% CI |
|---|---|---|---|---|---|
| \(t\) | 0.702 | 0.059 | -4.2 | 0.000 | 0.595 ; 0.828 |
| \(surgery(t=0)\) | 0.155 | 0.108 | -2.67 | 0.008 | 0.039 ; 0.609 |
| \(surgery\times t\) | 1.072 | 0.036 | 2.08 | 0.037 | 1.004 ; 1.145 |
| \(t^2\) | 1.013 | 0.005 | 2.37 | 0.018 | 1.002 ; 1.023 |
| \(t^3\) | 1.00 | 0.000 | -1.71 | 0.086 | 1.000 ; 1.000 |
| \(year\) | 0.872 | 0.064 | -1.86 | 0.062 | 0.755 ; 1.007 |
| \(age\) | 1.033 | 0.015 | 2.23 | 0.026 | 1.004 ; 1.063 |
| \(constante\) | 0.445 | 0.112 | -3.22 | 0.001 | 0.272 ; 0.728 |
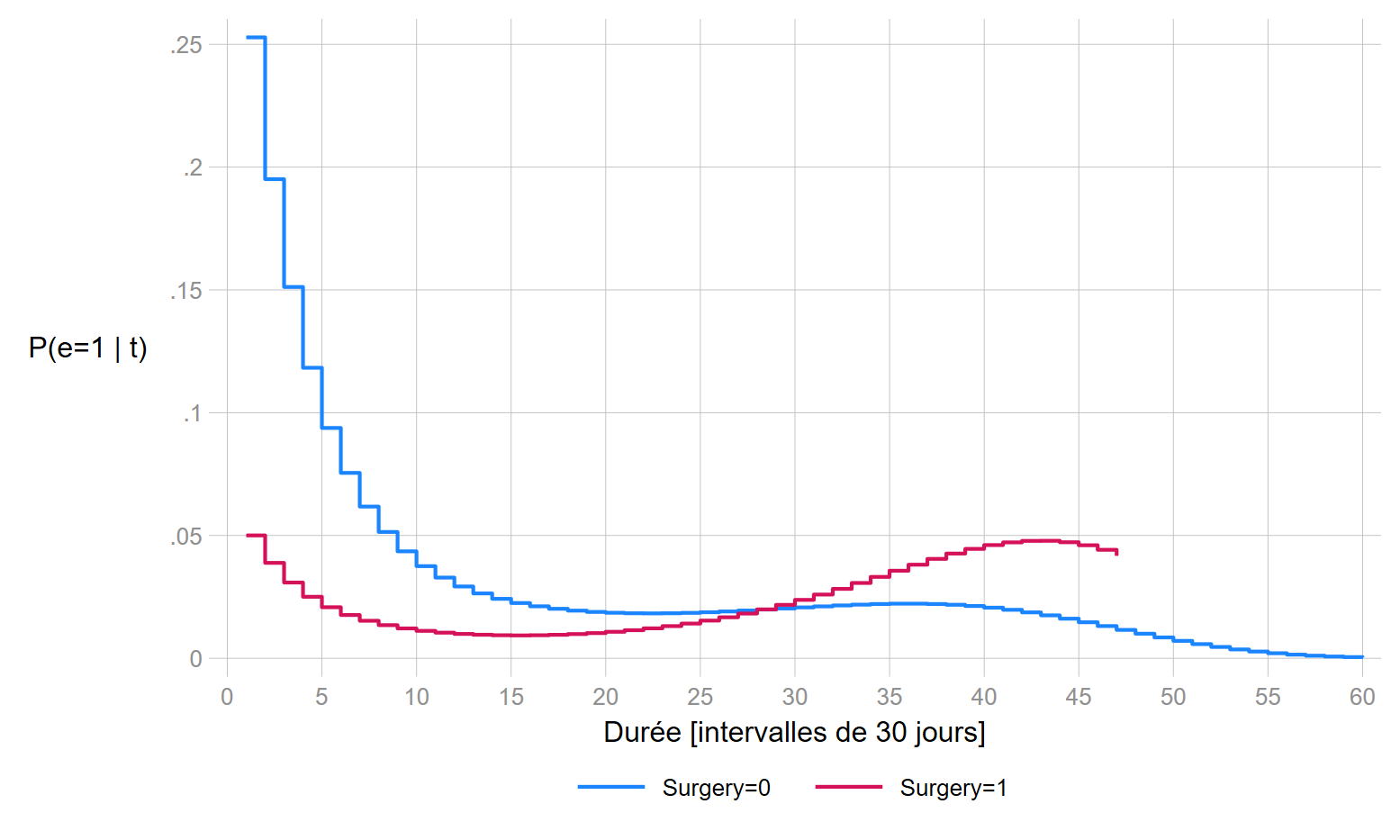
Avec une sépcification dépendant seulement de la durée (pour le graphique:
la distribution des probabilités sous cette loi n’est pas, contrairement aux lois normale ou logistique, symétriques. Dans ce qui suit, il n’est pas conseillé de l’utiliser dans l’application avec l’ajustement sous forme d’indicatrices avec seulement 4 intervalles↩︎
Non traité dans ce support, une méthode d’estimation en analyse de survie se nomme counting process et utilise des méthodes d’estimation de type poissonien↩︎
je remercie néanmoins Emilie Counil et Nargès Gouhoubi pour l’information↩︎
J’anticipe la version multinomiale pour les risques concurrents↩︎
Ce n’est pas le cas ici, mais si on sélectionne une forme cubique, je conseille vivement de regarder les probabilités conditionnelles prédites, en particulier en fin de périodes d’observation/exposition si peu d’individus restent soumis au risque. On peut rencontrer des problèmes d’overfitting avec des probabilités conditionnelles estimées trop proche de 1. Pour les personnes qui suivent la formation, c’est le cas avec les données des TP↩︎
Voir la très courte section sur les modèles paramétriques usuels↩︎