| Survival Status
| (1=dead)
compet | 0 1 | Total
-----------+----------------------+----------
0 | 28 0 | 28
1 | 0 56 | 56
2 | 0 19 | 19
-----------+----------------------+----------
Total | 28 75 | 103 12 Risques concurrents
Le problème des événements multiples dans les analyses de survie a été posé dans les années 1970 avec la notion de risques concurrents (competing risks) : il s’agit d’événements survenant au cours de la période d’observations et qui empêchent l’occurence de l’événement d’intérêt.
12.1 Problématique
On étudie un processus dont l’occurence a plusieurs modalités, types ou causes:
- La mortalité par cause de décès, les types de sortie du chômage: formation, emploi, radiation.
- Les types de sortie de l’emploi: chômage, longue maladie, sortie du marché du travail hors retraite.
- Les lieux de migration ou les espaces de mobilité résidentielle
- Les types de rupture d’union: séparation-divorce, veuvage).
Rappel: Déjà abordé dans la partie théorie, avec un recueil de données de type prospectif les “perdu.e.s de vue” peuvent difficilement être assimilés à des sorties d’observation non informatives (censures).
L’analyse des risques concurrents est un cas particulier des modèles multi-états avec différents risques considérés comme absorbants.
En présence de risques concurrents, l’estimation de Kaplan-Meier ne peut se faire que sous l’hypothèse d’indépendance entre chacun des risques. Sinon l’estimateur de Kaplan-Meier n’est plus une probabilité. Une estimation de type KM d’un évènement en concurrence avec d’autres impose que ces derniers soient traités comme des censures à droites non informatives. Mais il n’est pas possible de tester cette hypothèse.
12.2 Risques cause-specific et biais sur les estimateurs KM
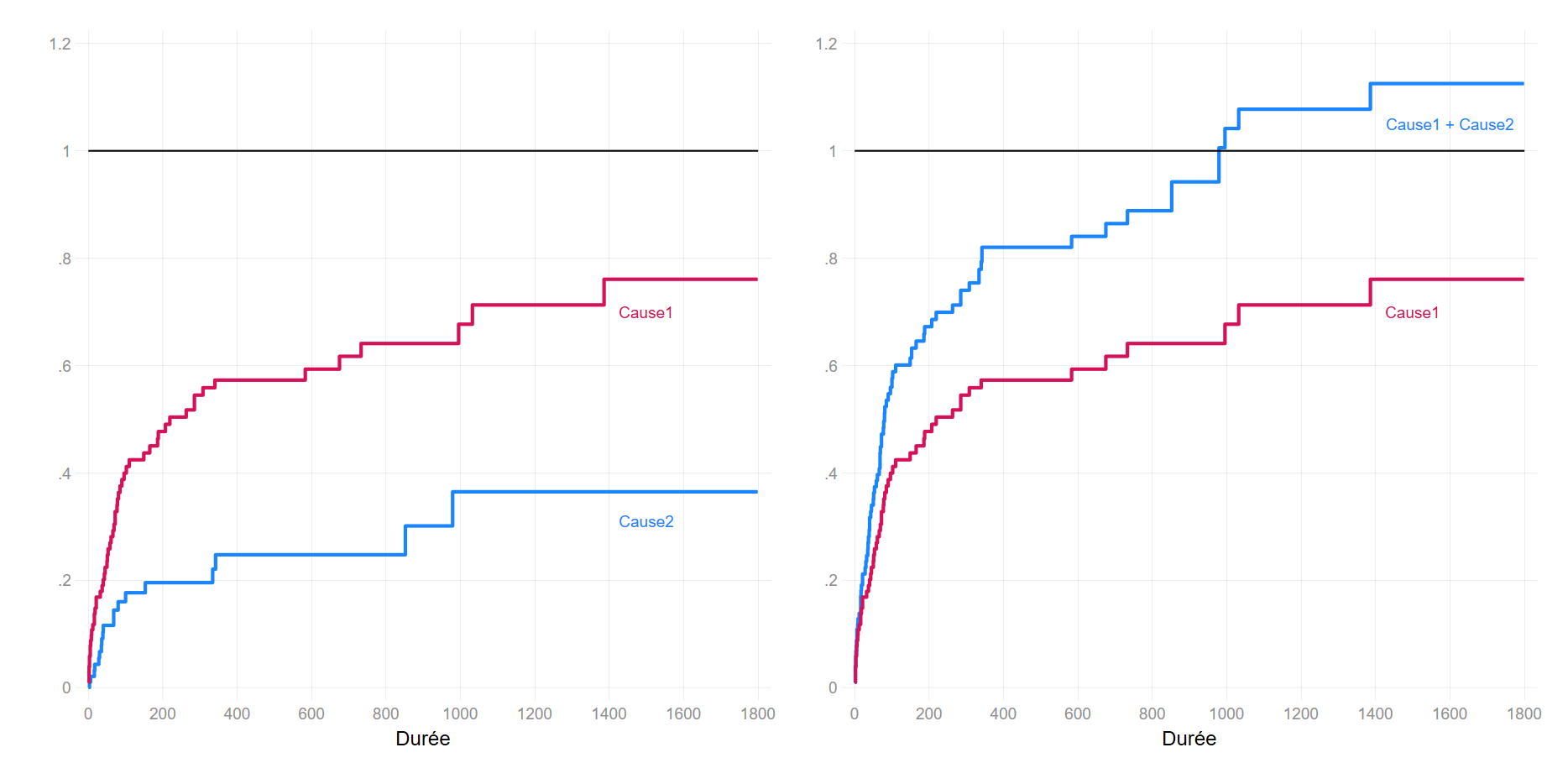
Si les risques ne sont pas indépendants les uns par rapport aux autres, la somme des estimateurs de (1-KM) pour chaque risque n’est pas égale - elle est supérieure - à l’estimateur de (1-KM) où les risques concurrents sont regroupés en un évènement unique. Par exemple les décès si on analyse ses causes.
Le risque calculé en considérant les risques concurrents comme des censures à droite est appelé “cause-specific risk.
Cause specific risk
Pour le risque de type \(k\), le risque cause-spécific en \(t_i\) est égal à:
\[h_k(t_i)=\frac{d_{i,k}}{R_i}\] Où \(d_{i,k}\) est le nombre d’évènement de type \(k\) survenu en \(t_i\) et \(R_i\) la population soumise en \(t_i\).
Conséquence: si les risques ne sont pas indépendants, la fonction de survie estimée avec la méthode Kaplan Meier n’exprime plus une probabilité.
Exemple sur les décès causés par une malformation cardiaque
Dans la base d’origine, il n’y a pas directement cette dimension de risque concurrent, même si on trouve dans la littérature médicale des études prenant le décès rapide post greffe comme un risque de ce type. Les données étant assez anciennes, avec beaucoup de décès post-opératoire, je ne me suis pas « risquer » à générer directement un risque concurrent sur cette information. Une sortie concurrente a donc été simulée sans plus de précision (variable compet), que l’on considèrera non strictement indépendante à la cause d’intérêt. Ce risque entre donc en concurrence avec la cause du décès directement liée à la malformation cardiaque, que la personne ait été transplantée ou non.
Variable compet:
cause 1 => décès directement provoquer par la malformation: compet=1 cause 2 => autre cause compet=0 => censure à droite
Lorsqu’on a analysé le décès par la méthode KM, la proportion de survivant.e.s était de 15%.
Si on applique la méthode de Kaplan Meier à la cause 1 en traitant la cause 2 comme une censure à droite (\(n=18+29=48\)), puis en sommant les deux estimateurs, la fonction de répartition excède 100% au bout de 1000 jours environs. La proportion de survivant.e.s est donc négative.
12.3 Estimations en présence de risques concurrents (CIF)
12.3.1 Estimation non paramétrique
- Utiliser l’estimateur de Nelson Aalen: il s’agit du risque instantané cumulé. Comme il ne s’agit pas d’une probabilité, il a été longtemps utilisé comme mesure de l’incidence en présence de risques concurrents dans une logique dite cause specific.
\[H_k (t_i)=\sum_{t_i\leq t}\left(\frac{e_{i,k}}{n_i}\right) \]
Actuellement, l’estimateur le plus utilisé est la fonction dite d’incidence cumulée - CIF- de Kalbfleisch-Prentice et Marubini-Valscchi:
- Il repose sur une probabilité tout en supportant la non indépendance des risques.
- Son interprétation est identique à la fonction de répartition \(F(t)=1-S(t)\). Cette fonction est donc croissante.
- Il est possible de tester les différences entres CIF: test de Gray (R, SAS) ou test de Pepe-Mori (Stata).
CIF (Cumulative Incidence Function)
- Si \(h_k(t_i)\) est le risque cause-spécific en \(t_i\) et \(S(t_i-1)\) l’estimateur de Kaplan-Meier en \(t_i-1\) lorsque tous les risques sont regroupés en un évènement unique, l’incidence cumulée pour le risque \(k\) en \(t_i\) est égale à:
\[IC_k(t_i)= \sum_{t_i\leq t}S(t_i-1)h_k(t_i)\]
- Les valeurs prises par cette fonction pour la cause \(k\) ne dépendent donc pas seulement des individus ayant observé l’évènement à partir de cette seule cause, mais aussi du nombre de personnes qui n’ont pas encore observés l’évènement à partir des autres causes identifiées. Cette dernière information est donnée par \(S(t_i-1)\).
- L’incidence cumulée peut ainsi s’interpréter, simplement, comme la proportion d’individus qui sont sortis du risque jusqu’en \(t_i\) en raison de la cause \(k\).
failure: compet == 1
competing failures: compet == 2
Time CIF SE [95% Conf. Int.]
--------------------------------------------------
1 0.0097 0.0097 0.0009 0.0477
2 0.0388 0.0190 0.0127 0.0892
3 0.0583 0.0231 0.0239 0.1149
5 0.0777 0.0264 0.0363 0.1395
6 0.0874 0.0278 0.0429 0.1515
8 0.0971 0.0292 0.0497 0.1634
9 0.1068 0.0304 0.0566 0.1751
12 0.1166 0.0316 0.0638 0.1868
16 0.1362 0.0338 0.0785 0.2099
18 0.1461 0.0349 0.0860 0.2212
21 0.1657 0.0367 0.1014 0.2437
32 0.1756 0.0376 0.1093 0.2550
37 0.1856 0.0384 0.1173 0.2662
40 0.1957 0.0393 0.1254 0.2775
43 0.2058 0.0400 0.1337 0.2888
45 0.2158 0.0408 0.1420 0.2999
50 0.2259 0.0415 0.1503 0.3110
51 0.2360 0.0422 0.1588 0.3221
53 0.2461 0.0428 0.1673 0.3330
58 0.2562 0.0434 0.1759 0.3439
61 0.2662 0.0440 0.1845 0.3548
66 0.2763 0.0445 0.1932 0.3656
69 0.2864 0.0450 0.2020 0.3763
72 0.3066 0.0459 0.2197 0.3976
77 0.3167 0.0464 0.2286 0.4082
78 0.3267 0.0467 0.2376 0.4187
81 0.3368 0.0471 0.2466 0.4292
85 0.3469 0.0475 0.2556 0.4396
90 0.3570 0.0478 0.2648 0.4500
96 0.3671 0.0481 0.2739 0.4604
102 0.3771 0.0484 0.2831 0.4707
110 0.3874 0.0487 0.2925 0.4812
149 0.3980 0.0489 0.3021 0.4920
165 0.4085 0.0492 0.3118 0.5027
186 0.4193 0.0495 0.3217 0.5137
188 0.4301 0.0497 0.3316 0.5246
207 0.4408 0.0499 0.3417 0.5354
219 0.4516 0.0501 0.3517 0.5462
263 0.4624 0.0502 0.3618 0.5570
285 0.4846 0.0505 0.3826 0.5791
308 0.4957 0.0506 0.3931 0.5900
340 0.5068 0.0507 0.4037 0.6009
583 0.5221 0.0514 0.4171 0.6168
675 0.5401 0.0524 0.4322 0.6361
733 0.5580 0.0532 0.4477 0.6548
995 0.5808 0.0548 0.4659 0.6795
1032 0.6036 0.0559 0.4851 0.7031
1386 0.6340 0.0583 0.5083 0.7357
failure: compet == 2
competing failures: compet == 1
Time CIF SE [95% Conf. Int.]
--------------------------------------------------
3 0.0097 0.0097 0.0009 0.0477
6 0.0194 0.0136 0.0038 0.0619
16 0.0292 0.0166 0.0079 0.0761
17 0.0391 0.0191 0.0128 0.0897
28 0.0489 0.0213 0.0182 0.1029
30 0.0587 0.0232 0.0240 0.1157
35 0.0686 0.0250 0.0302 0.1286
36 0.0786 0.0267 0.0367 0.1411
39 0.0885 0.0282 0.0435 0.1534
40 0.0986 0.0296 0.0504 0.1658
68 0.1188 0.0322 0.0650 0.1901
80 0.1288 0.0334 0.0724 0.2020
100 0.1389 0.0345 0.0800 0.2138
153 0.1495 0.0356 0.0880 0.2261
334 0.1605 0.0368 0.0964 0.2392
342 0.1720 0.0381 0.1052 0.2526
852 0.1913 0.0417 0.1175 0.2787
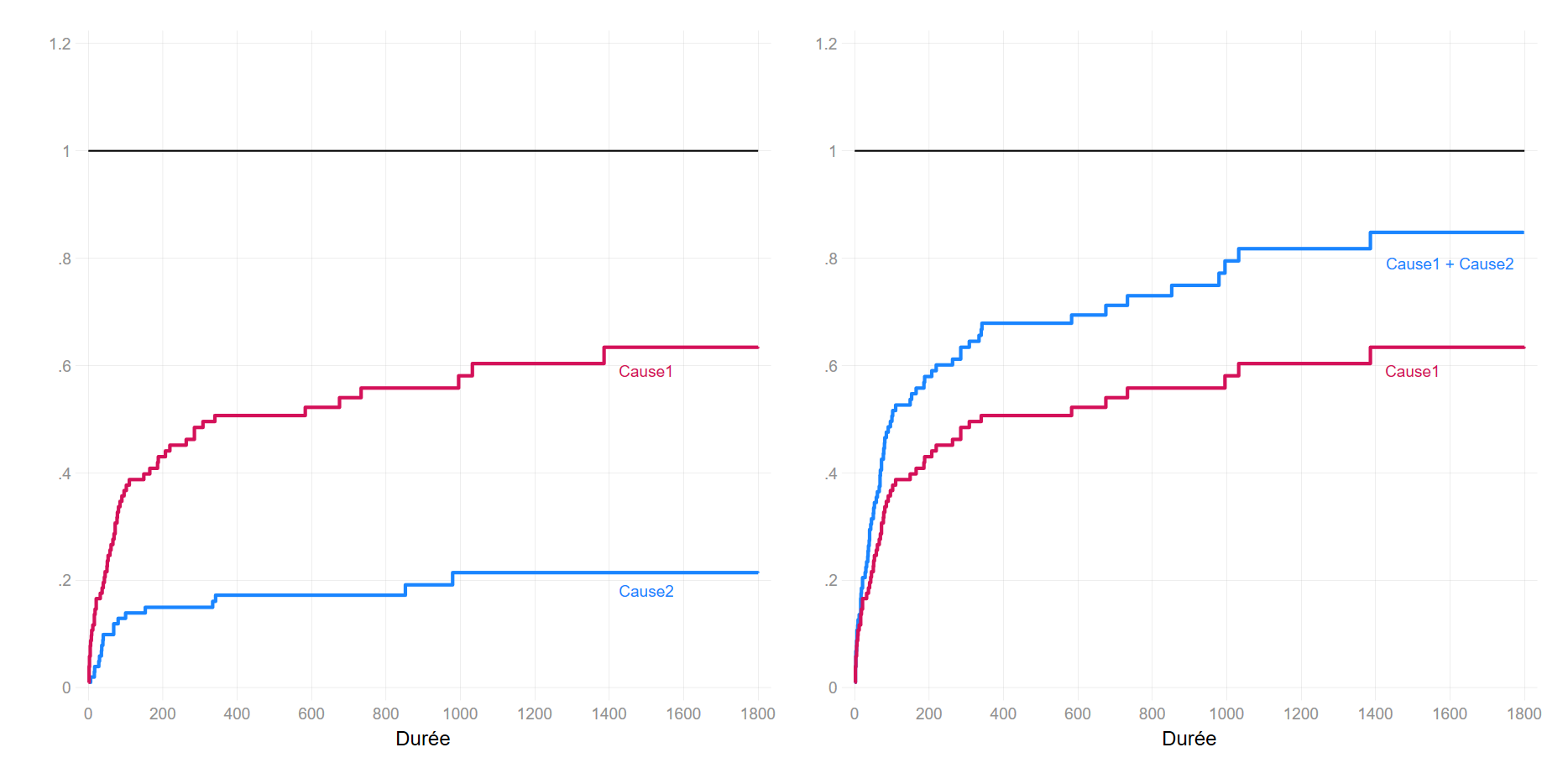
979 0.2141 0.0460 0.1320 0.3094En présence du risque concurrent, et traité comme tel, la moitié des personnes sont décédées suite à la malformation cardiaque au bout de 308 jours (200 jours avec une estimation de type « cause specific »).
On peut vérifier que la somme des estimateurs permet d’obtenir la survie toutes causes confondues. Il n’y a pas de surprise à cela, dans l’estimateur Marubini-Valscchi la survie d’ensemble intervient comme un facteur de pondération du quotient d’intensité dite « cause-specific ».
L’estimation avec des risques de type « cause-specific » demande juste de recoder la variable évènement/censure, en glissant les risques concurrents en censure à droite.
Pour l’estimation des CIF (risque de sous répartition):
R: la librairie
cmprskpermet d’estimer simplement les incidences cumulées avec la fonctioncuminc.Sas: maintenant directement estimable avec
proc lifetest. Il suffit d’indiquer le ou les risques d’intérêt dans l’instruction indiquant la variable de durée et de censure avec l’optionfailcode=valeur.Stata: Estimation avec la commande externe
stcompet. La commande génère des variables qui demande des manipulations supplémentaires pour afficher les résultats sous forme de tableau par exemple. On peut utiliser et préférer la commande externestcomlist.Python: le wrapper de R (
cmprsk) ne fonctionne plus à ce jour à défaut de mise à jour [2022].
12.3.2 Compararaison des CIF
Test d’homogénéité de Gray: est basé sur une autre mesure du risque en évènement concurrent. Sur le principe, identique à la philosopjie des test du logrank. Il s’agit du « subdistribution risks (« risque de sous-répartition », A.Latouche). Son interprétation n’est pas aisée car les personnes ayant observé un risque concurrent sont remises dans le Risk Set. Mais il est directement lié à l’estimation des CIF. Disponible avec SAS et R. Il est également sensible l’hypothèse de proportionnalité et à la distribution des censures à droites entre les groupes comparés. A ma connaissance il n’y a pas de variantes pondérées.
Test de Pepe & Mori: teste directement deux courbes d’incidences et seulement 2. Je n’ai pas le recul nécessaire sur cette alternative, qui n’est implémenté que dans Stata.
| Risques | Chi2 | P>Chi2 |
|---|---|---|
| Cause1 | 5.783 | 0.0161 |
| Cause2 | 0.129 | 0.7191 |
| Risques | Chi2 | P>Chi2 |
|---|---|---|
| Cause1 | 6.203 | 0.0127 |
| Cause2 | 1.880 | 0.7038 |
Sas: le test de Gray est estimé si on ajoute l’option strata=nom_variable à la proc lifetest sous risque concurrent (voir encadré précédent). Le test de Pepe-Mori est disponible via une macro externe (
%compcif: non testée) :Stata: Le test de Gray n’est pas disponible, il faut passer par une exécution de la fonction cuminc de la librairie R cmprsk directement dans stata (voir la commande
rsource). Pour faire plus simple, on peut estimer le modèle de Fine-Gray avec une seule variable (discrète). Le résultat est comparable à celui du test (voir plus bas). Le test de Pepe-Mori est disponible via la commande externestpepemori.R: On ajoute une variable à la fonction
cumincde la librairiecmprsk. Pas de test de Pepe-Mori sur les fonctions d’incidence à ma connaissance.Python: ne pas essayer d’utiliser la librairie cmprsk qui n’est pas mis à jour et ne fonctionne plus.
12.4 Modèles
12.4.1 Modèles Semi paramétriques
Cette présentation sera plutôt brève. Dans le domaine des sciences sociales, je préconise plutôt l’utilisation d’un modèle multinomial à temps discret de type logistique. Le modèle de Cox en présence de risques concurrent n’est valable que dans une logique de risques « cause-specific », le modèle de Fine et Gray bien que directement relié à l’estimation des incidences cumulées, repose sur une définition du risque (de sous répartition) dont l’interprétation n’est pas naturelle. Il est également soumis à l’hypothèse de proportionnalité des risques.
Modélisation des risques « cause-specific » : Cox
Modèle de Cox «standard» pour chaque évènement, les évènements concurrents sont traités comme des censures à droite. Aucune interprétation sur les fonctions d’incidence ne peut-être faite.
Modèle de Fine-Gray: subdistribution hazard regression
Modèle de type semi-paramétrique avec une redéfinition du risque lié à l’estimation des fonctions d’incidence (voir test de Gray). La différence avec le Cox classique réside dans le calcul du risk-set : les évènements concurrents ne sont pas considérés comme des censures, on laisse les individus leur « survivre » jusqu’à la durée maximale observée dans l’échantillon. L’interprétation n’est donc pas très intuitive (Fine et Gray le soulignent). Ce modèle est relativement contreversé. Il ne sera donc pas exécuté pour l’application
Pour les questions liées à l’interprétation de ces deux types de modèles, se reporter à: https://onlinelibrary.wiley.com/doi/epdf/10.1002/sim.7501
R: on utilise la fonction
crrdu package cmprsk.Sas: même principe que pour l’estimation non paramétrique, on ajoute l’option
eventcode=valeurà l’instructionmodelde laproc phreg.Stata: on utilise la commande interne
stcrreg.Python : ne pas essayer d’utiliser la librairie cmprsk qui n’est pas mis à jour et ne fonctionne donc plus.
12.4.2 Modèle à temps discret
Il s’agit d’une extension du modèle à temps discret à évènement unique (toutes causes regroupées) avec ici le modèle logistique multinomial.
S’il ne permet pas une interprétation sur les fonctions d’incidences, les risques concurrents ne sont pas traitées comme des censures à droite.
Le modèle multinomial repose sur une hypothèse dite « d’indépendance des alternatives non pertinentes » (IIA). Cela peut donc paraitre contradictoire d’utiliser ce modèle pour des évènements qui sont supposés non indépendants. Néanmoins la dépendance entre risques concurrents n’est pas non plus stricte et cette hypothèse d’IIA, seulement testable par le bon sens, est souvent illustrée par l’exemple des couleurs des bus dans le choix du mode de transport, ou les couleurs de chaussure dans les études marketing. Soit est une situation relativement limite.
En terme de lecture, les estiupateurs du modèle logistique multinomial peuvent directement s’interpréter comme des rapports de risque (ou relative risk ratio).
En sciences sociales, il me semble que ce type de modèle soit à privilégier.
On peut également envisager un modèle de type probit multinomial, mais on peut rencontrer des problèmes d’estimations (repose sur la loi normale multivariée). Prévoir un regroupement des causes concurrentes, et dans tous les cas de figure ne pas dépasser trois causes.
Niveau lecture, on peut utiliser une méthode de standardisation, de type AME (Average Marginal Effect).
Pour l’application, nous avons pris le mois (30 jours) comme métrique temporelle. On rappelle que les valeurs des estimateurs sont fictives en raison de la simulation des évènement pour le risque concurrent (cause2)
| Cause 1 | RRR | p>|z| | 95% IC |
|---|---|---|---|
| \(t\) | 0.816 | 0.000 | 0.752 - 0.885 |
| \(t^2\) | 1.003 | 0.000 | 1.001 - 1.005 |
| \(year\) | 0.879 | 0.116 | 0.749 - 1.032 |
| \(age\) | 1.045 | 0.012 | 1.010 - 1.081 |
| \(surgery\) | 0.318 | 0.033 | 0.110 - 0.913 |
| \(constante\) | 0.231 | 0.000 | 0.148 - 0.360 |
| Cause 2 | RRR | p>|z| | 95% IC |
|---|---|---|---|
| \(t\) | 0.817 | 0.003 | 0.713 - 0.935 |
| \(t^2\) | 1.003 | 0.052 | 1.000 - 1.006 |
| \(year\) | 0.816 | 0.141 | 0.622 - 1.070 |
| \(age\) | 1.011 | 0.654 | 0.964 - 1.061 |
| \(surgery\) | 0.541 | 0.431 | 0.117 - 2.496 |
| \(constante\) | 0.076 | 0.000 | 0.037 - 0.157 |
Notes:
- On a utilisé le terme RRR - Relative Risk Ratio - pour la colonne raportant les estimations. Dans un cadre de risque concurrent il est un peu difficile d’utiliser formellement la notion de hazard rate tel qu’il a été difini plus haut, enfin les modèles multinomiaux ne reportent pas formellement des Odds Ratios dont l’utilisation devrait être réservé exclusivement à une alternative binaire.
- les variables year et age ont été centrées sur leur valeur moyenne pour donner aux constantes des valeurs acceptables.
- Pour faciliter la lecture on peut utiliser une méthode de standardisation de type AME (Average Marginal Effect).